AIM2006ModulesBMM

From CNBH Acoustic Scale Wiki

AIM simulates the spectral analysis performed in the cochlea with an auditory filterbank, which is intended to simulate the motion of the basilar membrane (in conjunction with the outer hair cells) as a function of frequency and time. There is essentially no temporal averaging, in contrast to spectrographic representations where segments of sound 10 to 40 ms in duration are summarized in a spectral vector of magnitude values. Aim2006 simulates the basilar membrane motion (BMM) produced by the input sound with one of four filterbanks.

The default filterbank is dcgc: the dynamic, compressive gammachirp filterbank (Irino & Patterson, 2006). The dcgc filters have level-dependent asymmetry, and fast acting compression is applied between the first and second stages of the dcgc filter. The filter architecture and its operation are described below.

There are actually four auditory filterbanks available for different applications:

1. dcgc: The dynamic compressive gammachirp filterbank,
2. gc: The gammachirp filterbank: A time-domain version of the filter in Patterson et al. (2003),
3. wl: The wavelet filterbank: A time-domain version of the wavelet defined in Reimann (2006), and
4. gt: The gammatone filterbank: the traditional auditory filterbank of Patterson et al. (1995).
5. none: No auditory filterbank.

Background

Previous versions of AIM simulated the spectral analysis performed by the auditory system with a linear gammatone (GT) auditory filterbank (Cooke, 1993; Patterson & Moore, 1986; Patterson et al., 1992). There are three well known problems with using the GT filterbank as a simulation of cochlear filtering:

1. The filters were essentially symmetric on a linear frequency scale which is similar to the auditory filter at low stimulus levels. However, in the auditory system the filters become progressively broader and more asymmetric as level increases.
2. There is no compression in a GT filterbank. There is no compression in auditory filtering at high stimulus levels (above 85 dB SPL), but as level decreases the system applies more and more gain in the region of the tip of the filter which means that the input/output function of the basilar membrane (in combination with the outer hair cells) is strongly compressive. Previously in AIM, compression was applied as part of the transduction process that follows the GT filterbank.
3. Auditory compression is fast-acting; the compression varies dynamically within the glottal cycle. It compresses glottal pulses relative to the formant resonances that follow the glottal pulse. As a result, it restricts the dynamic range while maintaining good frequency resolution for the analysis of vocal-tract resonances (Irino & Patterson, 2006). It is argued that this dynamic adjustment of filter properties improves the robustness of speech recognition by raising the relatively low level of the formants with respect to the relatively high level of the glottal pulses. An extended example is presented in Irino and Patterson (2006, Figures 7, 8 and 9).

The compressive gammachirp filter

The compressive gammachirp (GC) filter is a generalized form of the gammatone filter, which was derived with operator techniques (Irino & Patterson, 1997). It was designed to simulate the properties of the auditory filter measured experimentally in the past 15 years. The development of both the gammatone and gammachirp filters is described in Patterson et al. (2003, Appendix A).

Figure 5. Illustration of (a) the construction of an asymmetric, passive gammachirp filter (GC) from a symmetric gammatone filter (GT) and a low-pass asymmetric function (LP-AF), and (b) the construction of a set of compressive gammachirp filters (GC) from one passive GC filter and a high-pass asymmetric function (HP-AF) whose center frequency shifts up as stimulus level increases. The vertical dotted lines show the peak frequencies of (a) the passive GC and GT filters (left and right, respectively) and (b) the passive GC filter. Figure from Patterson et al. (2003).

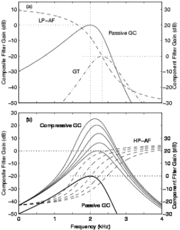
The compressive gammachirp (cGC) filter is composed of a passive gammachirp (pGC) filter and a High-Pass Asymmetric Function (HP-AF) arranged in cascade as shown in Figure 5 (Figure 1 in Patterson et al., 2003). The pGC filter simulates the action of the passive basilar membrane and the output of the pGC filter is used to adjust the level dependency of the active part of the filter, which is the HP-AF. The HP-AF is intended to represent the interaction of the cochlear partition with the tectorial membrane as suggested by Allen (1997) and Allen and Sen (1998). The effect is to sharpen the low-frequency side of the combined filter, which produces a tip in the cGC filter shape at low to medium stimulus levels (Figure.1a). Note, however, that there is no high-frequency side to this tip filter; it only produces high-pass filtering and level-dependent gain in the region of the peak frequency. The fact that there is no high-frequency side to the tip filter keeps the number of parameters to a minimum and avoids the instabilities encountered with the parallel filter systems where the high-frequency sides of the tip and tail filters interact.

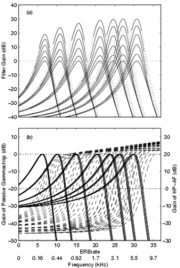
In Patterson et al. (2003), this cascade cGC filter was fitted to the combined notched-noise masking data of Glasberg and Moore (2000) and Baker et al. (1998). It was found that most of the effect of center frequency could be explained by the function that describes the c hange in filter bandwidth with center frequency. Patterson et al. (2003) expressed the parameters describing the filter as a function of ERBN-rate (Glasberg & Moore, 1990), where ERBN stands for the average value of the equivalent rectangular bandwidth of the auditory filter, as determined for young normally hearing listeners at mo derate sound levels (Moore, 2003). Once the parameters were written in this way, the shape of the cGC filter could be specified for the entire range of center frequencies (0.25-6.0 kHz) and levels (30-80 dB SPL) using just six fixed coefficients. The families of cGC filters derived in this way are illustrated in Figure. 6 for probe frequencies from 0.25 to 6.0 kHz.

Figure 6. Families of compressive gammachirp filters (a) for probe frequencies from 0.25 to 6.0 kHz. The component filters (b) are presented for four probe frequencies, 0.25, 1.0, 3.0 and 6.0 kHz; the remainder are omitted for clarity. The six curves within each set of cGC filters (a) and HP-AFs (b) show how the functions change as probe level increases from 30 to 80 dB in 10 dB steps. Figure from Patterson et al. (2003).

The cascade cGC filter has several advantages: (a) The compression it applies is largely limited to frequencies close to the center frequency of the filter, as happens in the cochlea (Recio, Rich, Narayan, & Ruggero, 1998); (b) The form of the chirp in the impulse response is largely independent of level, as in the cochlea (Carney, McDuffy, & Shekhter, 1999); (c) The impulse response can be used with an adaptive control circuit to produce a dynamic, compressive gammachirp filter (Irino & Patterson, 2005, 2006) to enable auditory modeling in which fast-acting compression is applied as part of the filtering process.

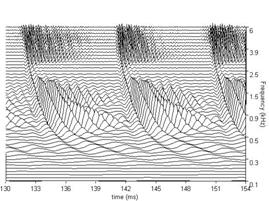
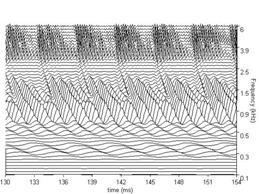
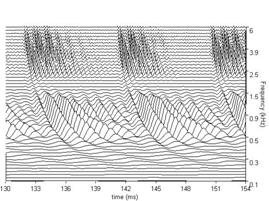
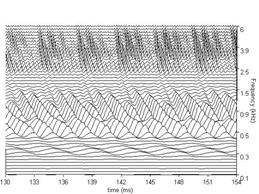
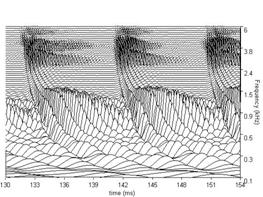
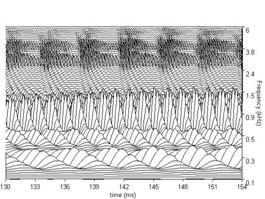
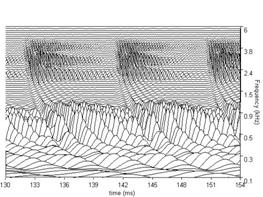
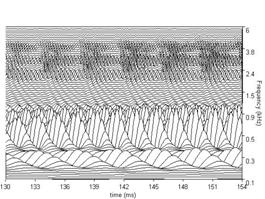
The BMM produced by the dcgc filterbank in response to each of the four /a/ vowels in Figure 3, is presented in Figure 7. The four subfigures show the BMM for the vowel in the corresponding subfigure of Figure 3. The concentrations of activity in channels above 0.5 kHz show the resonances of the vocal tract. They are the 'formants' of the vowel. The sinusoidal activity in the lowest channels represents the fundamental or second harmonic which is typically resolved for vowels; this activity is attenuated in the auditory system by the outer and middle ear transfer function which is simulated by the gm2002 option of the PCP modules. The duration of the segment of each panel of BMM is 24 ms. There are 100 channels in the filterbank in this example and they cover the frequency range of 100 to 6000 Hz. All of these parameters can be modified either directly in the control window or via the parameter file.

		BMM: dcgc
Resonance Rate (scale)	122
	89
		110	256
		Pulse rate (pitch)
Figure 7a. Basilar Membrane Motion(BMM) for the four example vowels produced by the dynamic compressive gammachirp filterbank. The subfigures are presented in the same format as in Figure 3. These plots are generated by choosing gm2002 in the PCP column and dcgc in the BMM column. See the text for details on the combinations of GPR and VTL.

Figure 7a shows the BMM for the four example vowels using the dcGC filterbank option; for comparison, Figure 7b shows the BMM for the same vowels using the gammatone filterbank. Note that there is a difference in the form and the relative strength of the formants; the dcGC filters are compressive and so the formant information is spread across more channels. The formants in the BMMs of the gammatone filters appear sharper at this stage. However, this apparent sharpness is spurious in the sense that this pattern does not actually occur on the basilar membrane. In traditional auditory models, the filterbank is linear and compression is applied at the output of the filterbank as if it were part of the neural transduction stage (described in 3.3 below). The dcGC filterbank may be unique in having fast-acting compression within the auditory filter, in a computational model. The differences in resonance rate are discernable in the low-pitch examples in the left-hand subfigures. The latency of the peaks that make up the ridges corresponding to the glottal pulses increase as frequency decreases. This is referred to as the propagation delay of the cochlea. Note, however, that the propagation delay is much less in the dcGC filterbank, so the channels are better aligned in time.

		BMM: gt
Resonance Rate (scale)	122
	89
		110	256
		Pulse rate (pitch)
Figure 7b. Basilar Membrane Motion (BMM) for the four example vowels produced by the traditional gammatone filterbank. The subfigures are presented in the same format as in Figure 3. These plots are generated by choosing gm2002 in the PCP column and gt in the BMM column. See the text for details on the combinations of GPR and VTL.

In Figures 7a and 7b, each plot has 100 frequency channels. The figures are generated using the MATLAB 'waterfall' plotting function, and then exported as jpg files. The default plot type in aim2006 for the BMM stage is actually 'mesh', because it renders much faster, and for most everyday uses, its resolution is sufficient. It is also sometimes useful to reduce the number of frequency channels to 50 to achieve faster graphics rendering. When high-quality figures are required for printed presentation or videos, the plot type can be changed to 'waterfall’ in the file parameters.m for the graphics module in question (e.g. /aim-mat/modules/graphics/dcgc/ for the dcgc filterbank).