Category:Introduction to Communication Sounds
From CNBH Acoustic Scale Wiki
The sounds that animals use to communicate at a distance, to declare their territories and attract mates, are typically pulse-resonance sounds. These sounds are ubiquitous in the natural world and in the human environment. They are the basis of the calls produced by most vertebrates (mammals, birds, reptiles, frogs and fish); they are also the basis of many invertebrate communication sounds, such as those of the insects and the crustaceans. Although the structures used to produce pulse-resonance sounds can be quite elaborate, the mechanism is conceptually very simple. The animal develops some means of producing an abrupt pulse of mechanical energy which causes structures in the body to resonate. With regard to information, the pulse signals the start of the communication and the resonance provides distinctive information about the shape and structure of the sounders in the sender’s body, and thus, distinctive information about the species producing the sound. The category Information in Communication Sounds focuses on the distinction between the message of a communication sound and the size information in the wave that carries the message from the sender to the listener. Those who do not have a background in perception might like to start with an introduction auditory perception – a parallel stream of the wiki.
Contents |
Communication Sounds
The pulse-resonance mechanism
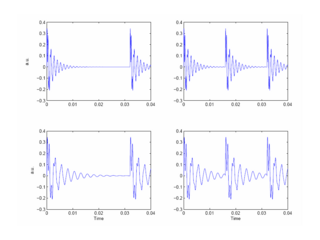
For humans, the most familiar communication sound is speech and the voiced parts of speech are classic pulse-resonance sounds. The vocal folds in the larynx at the base of the throat produce pulses of acoustic energy by momentarily impeding the flow of air from the lungs, and each of these ‘glottal pulses’ then excites a complex of resonances in the vocal tract above the larynx. The two resonances, or formants, with the lowest centre frequencies carry the most information in speech, and a set of four synthetic, two-formant vowels shown in Figure 1 will be used to illustrate the form of acoustic scale information in communication sounds.
The pulse period of the two vowels in the left-hand column is 32 ms; the pitch is 31.25 Hz which is very close to the lower limit of temporal pitch. The pulse period in the right-hand column is 16 ms; the pitch is 62.5 Hz which is typical of a large man with a deep voice. The formants are simple damped resonances centred at 400 Hz and 1257 Hz for the vowels in the lower row of the figure, and at 800 Hz and 2514 Hz for the vowels in the upper row. So, the formant frequencies are not harmonically related, but the formant frequency ratio is the same for all four vowels, and they all sound roughly like the /a/ in ‘brought’. The figure shows that vowels are glottal pulses with complex resonances attached. The message of the vowel is contained in the shape of the resonance which is the same in each cycle of each vowel. The bandwidths of the formants are proportional to their centre frequencies, which means that the upper formant decays faster than the lower one in each case. The two formants can be observed interacting in the first couple of cycles at the start of each resonance; thereafter, the resonance of the lower formant dominates the waveform. One of the problems for the auditory system is to extract a good estimate of the second formant given the dominance of the first formant in the waveform.
Many of the musical instruments that humans have developed to communicate musically also produce pulse-resonance sounds: The percussive instruments (drums, chimes, glockenspiels etc) produce single-cycle, pulse-resonance sounds; the sustained-tone instruments (brass, strings, woodwinds) produce notes whose internal structure is similar to vowels. In music, the ‘message’ of a note is the timbre of the sound, that is, the distinctive sound of the instrument family, and this family message is conveyed by the resonance shape.
There is a page which discusses the form of pulse-resonance sounds where it is argued that they are an efficient, relatively simple solution to the problem of bio-acoustic communication, and that nature has repeatedly developed pulse-resonance communication using a wide variety of structures in unrelated groups of animals. The evidence that there has been parallel, convergent evolution of pulse-resonance communication in a variety of animals suggests that there is something fundamentally adaptive about the production and perception mechanisms that underlie this mode of communication.
The effect of source size in pulse-resonance sounds
In the majority of animals, nature has adapted existing body parts to create the structures that animals use to produce their sounds. In mammals, for example, the vocal tract is based on the tubes that carry air and food from the entrance of the nose and mouth to the lungs and stomach, respectively. As the animal grows, these tubes have to get longer to keep the nose and mouth connected to the lungs and stomach. As the tubes get longer, the resonators in the vocal tract get larger and ring more slowly. Similarly, as the vocal tract gets wider, the vocal cords get longer and more massive, which means that the glottal pulse rate decreases as the animal grows. The sound producing mechanism typically maintains its overall shape and structure as the individual grows. As a result, the population of calls produced by a species all have the same message, but the message is carried by sounds that vary in their resonance rate and their pulse rate.
The vowels in Figure 1 are intended to illustrate the effect of growth on pulse-resonance sounds: The shape of the resonance is the same in every cycle of all four panels and so the vowel type is the same in each case. The vowel in panel (c) is characteristic of an adult with large vocal cords and a long vocal tract. The vowel has a low pulse rate and a slow resonance rate, that is, the rate of cycles in the resonance is slow (relatively). The vowel in the upper right panel is like the vowel of a child, produced with smaller vocal cords and a shorter vocal tract. Both the pulse rate and the resonance rate are greater in this vowel. Indeed, the adult vowel (panel b) is actually a scaled version of the juvenile vowel (panel b). It is as if we had recorded a child’s voice and simulated the adult’s voice simply by reducing the speed of the recording on playback; the ratio of the pulse rates for the vowels in panels (b) and (c) is the same as the ratio of the resonance rates in these panels. If the adult sound wave is SndAdult(t) and the juvenile sound wave is SndChild(t), then SndAdult(t) = SndChild(at), where a is the scalar. The example illustrates the concept of acoustic scale in the time domain, and the fact that a change in the size of the source produces a change in the scale of the sound that the source produces. There are two components to the acoustic scale information: the period of the sound is the acoustic scale of the excitation source (the vocal cords); the resonance rate reflects the acoustic scale of the resonances in the vocal tract (the frequencies of the formants of the vowel). There is a page which provides an extended discussion of acoustic scale in the waves and spectra of communication sounds.
In communication sounds, although both the pulse rate and resonance rate are correlated with the size of the source, they are largely independent variables. The vowel in panel (a) has the pulse rate of the adult and the resonance rate of the child; it sounds a bit like a dwarf. The vowel in panel (d) has the pulse rate of the child and the resonance rate of the adult; it sounds a bit like a counter tenor. Despite the marked differences in the pulse and resonance rates, we hear both the dwarf and the counter tenor as saying pretty much the same vowel as the adult and the child. The figure emphasizes that the message of the vowel (resonance shape) can be conveyed by sounds with a wide range of pulse rates and a wide range of resonance rates.
The properties of vowels illustrated in Figure 1 are also characteristic of the communication sounds of other animals; they also produce pulse-resonance sounds. In this case, the message is the species of the sender and it can be conveyed by a population of individuals with varying sizes. As a result, the message is carried by sounds with different pulse rates and resonance rates, as with vowel sounds. Similarly, the instrument-family information in a musical note (e.g., brass or woodwind) is associated with the resonance shape, and this family information can be conveyed by family members with different sizes (e.g., trumpet, trombone and tuba, or oboe and bassoon). The members produce sounds with different resonance rates, and they can do so with notes having a range of different pulse rates.
The discrimination/generalization problem in communication
The fact that members of a species communicate their presence using calls that vary in pulse rate and resonance rate presents the listener with a classic categorization problem – how to discriminate different species and, at the same time, correctly generalize across calls within a species. Distinguishing two sounds is not difficult, especially when they vary in pulse rate and resonance rate. The generalization problem involves isolating the resonance shape and recognizing that the calls of large and small members of the species are ‘the same’ despite the fact that the calls are carried by sounds with different pulse rates and different resonance rates. The discrimination problem involves recognizing that two calls with the same pulse rate and similar resonance rates may, nevertheless represent two different species because their resonance shapes are different.
The discrimination/generalization problem is exacerbated by the fact that pulse rate is also affected by the tension of the vocal cords, and the tension is varied voluntarily by many animals, and this ‘prosody’ information is part of their communication. Pulse rate is perceived by humans as voice pitch in speech sounds and melodic pitch in musical sounds. For purposes of this introduction, however, the variability introduced by voluntary manipulation of pulse rate can be grouped with the variability associated with size as a component of pulse-rate variability. The variability contributes in the same way to the discrimination-generalization problem no matter what its source. It is also the case that the pulse-resonance sounds of cold-blooded animals change their acoustic scale with temperature. But again, the effect is to change the scale of the pulse rate and the scale of the resonance rather than its shape, and all of the scale changes affect the discrimination/generalization problem in the same way.
Body size, resonator size and acoustic scale
In the discussion above, and in what follows, we often talk about the size of the source and the effect of source size on the communication sounds that they produce, and the interpretation of those sounds by the auditory system and the brain of the receiver. For example, when a person listens to a stranger on the telephone, they have a distinct impression of the size of the speaker. With regard to perception, it is important to distinguish between body size, resonator size and acoustic scale. It is the size of the resonators in the speaker's vocal tract that determines the resonance rate, or acoustic scale, of their voiced sounds, rather than the size of the speaker's body (i.e., their height). But vocal-tract length and resonator size are highly correlated with speaker height and so it is not surprising to find that the brain interprets acoustic scale in terms of body size. The brain is not really interested in intervening variables like vocal tract length or the speed of sound; it treats the process of communication as a black box. It is the height of the source that matters for fight or flight decisions. So the listener does not perceive the acoustic scale of the resonators in a source in terms of a resonance rate or a vocal tract length; it perceives acoustic scale in terms of the size of the body of the speaker.
The Perception and Processing of Communication Sounds
Auditory perceptions are constructed in the brain from sounds entering the ear canal, in conjunction with current context and information from memory. It is not possible to make direct measurements of perceptions, so all descriptions of perceptions involve explicit, or implicit, models of how perceptions are constructed. The category Auditory Processing of Communication Sounds focuses on how the auditory system might construct your initial experience of a sound, referred to as the 'auditory image'. It describes a computational model of how the construction might be accomplished -- the Auditory Image Model (AIM). The category Perception of Communication Sounds focuses on the structures that appear in the auditory image and how we perceive them.
The perception of communication sounds
It is assumed that your sensory organs and the neural mechanisms that process sensory data together construct internal, mental models of external objects in the world around us; the visual system constructs a visual object from the light the object reflects and the auditory system constructs an auditory object from the sound the object emits, and these objects are combined with any tactile and/or olfactory information (which might possibly also be thought of as tactile and/or olfactory objects) to produce our experience of an external object. Our task as auditory neuroscientists is to characterize the auditory part of this object modelling process. This subsection of the introduction sets out the basic assumptions of AIM with the terms required to understand this conception of the internal representation of sounds.
It is assumed that the sub-cortical auditory system creates a perceptual space, in which an initial auditory image of a sound is assembled by the cochlea and mid-brain using largely data-driven processes. The auditory image and the space it occupies is analogous to the visual image and space that appear when you open your eyes in the morning. If the sound arriving at the ears is a noise, the auditory image is filled with activity, but it lacks organization and the details are continually fluctuating. If the sound has a pulse-resonance form, an auditory figure appears in the auditory image with an elaborate structure that reflects the phase-locked neural firing pattern produced by the sound in the cochlea. Extended segments of sound, like syllables or musical notes, cause auditory figures to emerge, evolve, and decay in what might be referred to as auditory events, and these events characterize the acoustic gestures of the external source. All of the processing up to the level of auditory figures and events can proceed without the need of top-down processing associated with context or attention. It is assumed, for example, that auditory figures and events are produced in response to sounds when we are asleep. And, if we are presented with the call of a new animal that we have never encountered before, the early stages of auditory processing will still produce an auditory event, even though we (the listeners) might be puzzled by the event.
Subsequently, when alert, the brain may interpret the auditory event, in conjunction with events in other sensory systems, and in conjunction with contextual information that gives the event meaning. At this point, the event with its meaning becomes an auditory object, that is, the auditory part of the perceptual model of the external object that was the source of the sound. An introduction to auditory {objects, events, figures, images and scenes} is described in the paper entitled Homage à Magritte: An introduction to auditory objects, events, figures, images and scenes . It is a revised transcription of a talk presented at the Auditory Objects Meeting at the Novartis Foundation in London, 1-2 October 2007.
Auditory processing of communication sounds
The main focus of the category Auditory Processing of Communication Sounds is the form of auditory images: how they are constructed from the neural activity pattern (NAP) of a sound flowing from the cochlea and the events that arise in this space of auditory perception in response to communication sounds. It appears that the space of auditory perception is rather different from the {time, frequency} space normally used to represent speech and musical sounds, and the auditory events that appear in the auditory space are very different from the smooth energy envelopes that represent events in the spectrogram. Briefly, it appears that the space of auditory perception has three dimensions, linear time, logarithmic scale and logarithmic cycles, which will be explained below. The {log-scale, log-cycles} plane of the space is obtained through a unitary transform of the traditional {linear-time,linear-frequency} plane, and the auditory figures that appear in this new plane have the property of being scale-shift covariant (ssc), with regard to both resonance rate and pulse rate. Moreover, the three forms of information in communication sounds are largely orthogonal in this plane. The advantage of the auditory space is that the message of a communication sound appears in a form that is essentially fixed, independent of the pulse rate and the resonance rate of the sound that conveys the message. It also appears that scale-shift covariance of this form is not mathematically possible in a {linear-time, linear-frequency} representation like the spectrogram. If this is the case, then it is important to understand scale-shift covariance and the space of auditory perception in order to improve the robustness of computer-based, sound processors like speech recognition machines and music classifiers.
The robustness of perception to variation in acoustic scale
Perceptual experiments with communication sounds show what everyone intuitively knows; auditory perception is singularly robust to changes in both the resonance rate and the pulse rate of a communication sound. The experiments show that we have no difficulty whatsoever understanding when a child and an adult have spoken the same speech sounds (syllables or words), despite substantial differences in pulse rate and resonance rate of the waves carrying the message. We also know which speaker has the higher pitch and which speaker is bigger (i.e., which speaker has the longer vocal tract). Perceptual experiments have been performed with vowels, musical notes and animal calls; they all lead to the conclusion that auditory perception is singularly robust to the scale variability in communication sounds. It is also the case that the robustness of human perception extends to speech sounds and musical sounds scaled well beyond the range of normal experience, which suggests that the robustness is based on automatic adaptation or normalization mechanisms rather than learning. The basic experiments on the perception of source size are described in the category Perception of Communication Sounds. The normalization mechanisms are described in the category Auditory Processing of Communication Sounds.
The robustness of auditory perception stands in contrast to the lack of robustness in mechanical speech recognition systems; a speech recognizer trained on the speech of a man is typically not able to recognize the speech of a woman, let alone the speech of a child. Thus, the robustness which we take for granted and think of as trivial, poses a very difficult problem if it is left to the recognition system that follows the pre-processor to learn about pulse rate and resonance rate variability from a time-frequency representation like the spectrogram. The category HSR for ASR focuses on the application of knowledge about Human Speech Recognition (HSR) to Automatic Speech Recognition (ASR). The main concerns are developing Auditory feature vectors that improve the robustness of ASR, and estimating vocal tract length from individual vowel sounds
Scale-Shift Covariance: the key to robustness in perception
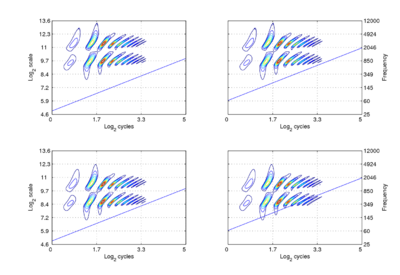
The form of communication sounds and the robustness of auditory perception suggest that the internal representation of communication sounds is somehow ‘shift covariant’ both to changes in resonance rate (scale-shift covariance) and pulse rate (period-shift covariance). If the space of auditory perception already has these properties, then more central mechanisms will not need to learn about the variability that arises in {time, frequency} space, and this would go some way to explaining our facility with speech and language, and our ability as children to learn language from people of widely differing sizes. The mathematical definitions of ‘covariance’ and ‘shift-covariance’ are beyond the scope of this introduction to auditory processing; they are defined and discussed in a recent paper entitled The robustness of bio-acoustic communication and the role of normalization. The concept of shift covariance and its value in modelling auditory perception can be illustrated using simulated auditory images of the four synthetic vowels of Figure 1 above; the auditory images are shown in Figure 2.
The dimensions of the plane are scale and cycles in {log2(cycles), log2(scale)} form. The important points to note at this juncture are the following: The pattern of activation that represents the message – the auditory figure – has a fixed form in all four panels; it does not vary in shape with changes in pulse rate or resonance rate. When there is a change in resonance rate (vocal tract length) from small to large, the activity just moves vertically down as a unit without deformation; compare the auditory figures in the panels of the upper row to those in the panels of the lower row. The extent of the shift is the logarithm of the ratio of the resonance rates of the sources. When there is a shift in pulse rate from longer to shorter, the auditory figure does not change shape and it does not move vertically; rather, the diagonal which marks the extent of the pulse period, moves vertically without changing either its shape or its angle. This changes the size of the area available for auditory figures, but does not change the shape of the figure, other than to cut off the tails of the resonances when the pulse period is short relative to the resonance duration. The extent of the vertical shift of the diagonal is the logarithm of the ratio of the pulse rates of the sources. Since the pulse rate and the resonance rate were both scaled by the same amount in this example, the vertical shift (between rows) of the auditory figure and the vertical shift of the period-limiting diagonal (between columns) are the same size.
Comparison of panel (a) with panels (b) and (c), and comparison of panel (d) with panels (b) and (c), show that the shift covariance property applies separately to the pulse rate and the resonance rate, albeit in a somewhat different form. The independence is important because, although pulse rate and resonance rate typically covary with size as members of a population of animals grow, the correlation in growth rate is far from perfect. For example, in humans, both pulse rate and resonance rate decrease as we grow up; however, whereas VTL is closely correlated with size throughout life, in males, pulse rate takes a sudden drop at puberty.
The figure also illustrates one of the constraints on pulse-resonance communication; although the auditory image itself is rectangular, the auditory figures of pulse-resonance sounds are limited to the upper triangular half of the plane. The lowest component of a sound cannot have a resonance rate below the pulse rate of the sound.
Intuitively, this auditory plane and the auditory figures that arise in it provide a better basis for a model of auditory perception than the traditional {time, frequency} space and the traditional spectrographic representation of speech, inasmuch as the auditory space appears to be able to explain why it is that we can hear the message of a communication sound independent of the size of the sender. If this is the space of auditory perception rather than a {time, frequency} space, and if the mechanisms are inherited and develop as a part of the auditory system, this would help to explain how children manage to learn speech in a world where the samples they experience come from people of such different sizes (parents and siblings). It would also help explain how animals with much smaller brains and shorter life spans than those of humans manage to cope with the size variability in the communication sounds or their species and other species.
The figure also suggests that it may well be possible to produce a speech pre-processor for ASR systems that automatically performs, speaker-independent, vocal-tract-length normalization which should improve ASR performance. The category HSR for ASR focuses on the application of knowledge about Human Speech Recognition (HSR) to Automatic Speech Recognition (ASR). It includes a paper on the developement of Auditory features that are robust to changes in speaker size.
The space of auditory perception
In the auditory image model of perception, it is argued that the cochlea and midbrain together construct the auditory image in a {linear-time, log2(cycles), log2(scale)} space. Briefly, the basilar membrane performs a wavelet transform which creates the acoustic scale dimension of the auditory image (the vertical dimension). It is the 'tonotopic' dimension of hearing and it is a close relative of the traditional frequency dimension but it is fundamentally logarithmic. The acoustic scale dimension is critical to auditory perception, but the basis of perception is not simply a time-scale recording of basilar membrane motion (BMM). The inner hair cells and primary nerve fibres convert BMM into a two-dimensional pattern of peak-amplitude times, and it is this neural activity pattern (NAP) that flows up the auditory nerve to the brainstem, rather than the BMM itself. The NAP is a time-scale representation of the information in the sound that can be observed physiologically in the auditory nerve and cochlear nucleus. However, the basis of perception cannot be the NAP itself, since it would appear that our initial auditory images are scale-shift covariant, and time-scale representations like the NAP are not scale-shift covariant, by their nature. It appears that a third, time-interval, dimension is added to the NAP to produce the scale-shift covariant auditory image (sscAI). The addition of the extra dimension to the space of auditory perception is described on a separate page, The Space of Auditory Perception. The addition of the 'cycles' dimension to the time dimension and the acoustic scale dimension provides a space that would appear to have the properties necessary to explain the robustness of auditory perception. The Space of Auditory Perception is an early version of The robustness of bio-acoustic communication and the role of normalization with the emphasis on perception rather than source normalization.
Evolution of pulse-resonance communication (under construction)
The size-shift-covariant auditory image (sscAI), and the description of how it might be constructed, have been presented largely from the perspective of human speech perception, and what makes it robust to changes in acoustic scale. We attempted to motivate the need for shift covariance by explaining that the communication sounds of a population of animals must vary in acoustic scale because the sound generators are integral parts of the body, and that perceptual robustness requires the appropriate processing of scale information. Nevertheless, the proposed perceptual solution – a scale shift covariant auditory image – might seem rather fantastic to some readers, and they might wonder how something so unusual could possibly have developed. In point of fact, from the information processing point of view, the evolution of pulse-resonance communication would appear to be relatively straightforward, and the prevalence of pulse-resonance communication in the natural world suggests that it probably evolved separately, a number of times, in widely divergent groups of animals.
Although it is not necessary to explain the evolution of hearing in order to study auditory perception, it might be reassuring to know that it is quite simple to implement size-shift covariance in neural processing. Accordingly, the category Evolution of Communication Sounds is intended to provide a brief overview of how acoustic communication might have evolved. The text is currently under construction.
Brain Imaging of Communication Sound Processing
Currently this category just contains a list of brain imaging papers. When resources permit, a text will be written to explain the Brain Imaging of Communication Sound Processing which will summarize recent experiments designed to locate regions activation associated with the processing of communication sounds.
References
- Patterson, R.D., van Dinther, R. and Irino, T. (2007). “The robustness of bio-acoustic communication and the role of normalization”, in Proceedings of the 19th International Congress on Acoustics, p.07-011. [1]
This category currently contains no pages or media.