Estimating Vocal Tract Length from a Stream of Vowel Sounds
From CNBH Acoustic Scale Wiki
J.J.M. Monaghan, G.J. Kerr, A. Mahakuperan, T.C. Walters, C. Feldbauer, R.D. Patterson.
Perceptual experiments reveal that there is size information in speech sounds; humans can easily distinguish between individuals with different vocal tract lengths (VTL) and discriminate their relative sizes. The auditory image model (AIM) simulates the processing of the human auditory system and produces a representation of sound in which changes in VTL produce predictable shifts of the speech pattern in the representation. Accordingly, AIM was used as the pre-processor for a system designed to estimate the vocal tract length of a speaker on a frame by frame basis from a stream of continuous speech. The system (1) constructed feature vectors from individual frames of AIM-processed speech, (2) established whether the frame contained a strong vowel sound, and if so, (3) used the feature vectors to provide an estimate of the VTL of the speaker. The vocal tract length estimates produced by these estimators can be converted to height estimates using the magnetic resonance imaging data of Fitch and Giedd (1999). The purpose of the system is to provide a tracking variable for speech recognition software or for forensic identification. The system was tested using scaled versions of the speakers used in training; the system was found to achieve a level of performance close to that of humans.
The text and figures on this page are from a project report associated with an EOARD grant (FA8655-05-1-3043) entitled Measuring and Enhancing the Robustness of Automatic Speech Recognition
Roy Patterson , Jessica Monaghan , Tom Walters
Contents |
Introduction
When we listen to speech, we can hear, without effort, both the semantic content of the sound and properties of the speaker’s voice. In particular, speech contains information about the vocal tract length (VTL) of the speaker and the rate of opening and closing of the vocal folds – the glottal pulse rate (GPR) which we interpret as the pitch of the speaker. Alongside these speaker characteristics a listener extracts the syllable information, which is the bulk of the semantic content in short segments of speech. Human speech is an example of a ‘pulse-resonance’ communication sound, typified by a sequence of sharp glottal pulses, each directly followed by a vocal tract resonance. The glottal pulses carry little information on their own; they mainly serve to mark the beginning of the resonance. The resonances represent the information about the structure and size of the source. The shape of these resonances may be characterised by formants, which are a series of increasing frequencies f1, f2, ..., fn corresponding to successive peaks in the frequency spectrum of a resonating object – here, the vocal tract. Particular vowels have characteristic spectral profiles and may be described in terms of their formants.
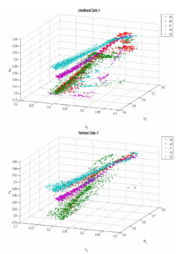
As well as the shape of the vocal tract, formant frequencies are affected by vocal tract length. Say a given speaker has VTL, L, and a frequency response to a pulse of H(ν). If this speaker is VTL-scaled to L′ = L/α, where α is a scaling constant, the frequency response becomes H′(ν) =H(αν). When plotted on a logarithmic frequency scale, such as the ERB scale used in AIM, the frequency dilation produced by a change in speaker size becomes a nearly linear shift of the spectrum, as a unit, along the axis – towards the origin as the speaker increases in size (see Figure 1).

Psychoacoustic studies have documented the ability of listeners to judge the relative size of speakers with different vocal tract lengths as well as to understand their speech (e.g., Ives et al., 2005). Fitch and Giedd (1999) demonstrated, using magnetic resonance imaging (MRI), that vocal tract length (VTL) is strongly correlated with height in humans, which suggests there would be an evolutionary advantage to being able to extract VTL information from speech. It also means that a device for estimating vocal tract length from samples of a person’s speech could predict their height, and therefore be useful as a forensic tool. Unfortunately, the error involved in the conversion from VTL to height is quite large (±9cm), which restricts that accuracy of height estimates. However, if a stable estimate of VTL can be produced for each speaker in an environment, the estimates would be very useful as tracking variables in ASR, as they would assist differentiation between speakers and separation of concurrent speech into speaker-specific streams. For this purpose the system would simply need to determine when the VTL estimate had changed sufficiently to indicate a new speaker.
AIM Feature Vectors
The Auditory Image Model (AIM) (Irino and Patterson 2002) simulates the auditory processing that is applied to speech sounds, as they proceed up the auditory pathway to the speech specific processing centers in the temporal lobe of cerebral cortex. AIM produces a pitch-invariant, size-covariant representation of sounds referred to as the size-shape image (SSI). This representation includes a simulation of the normalization for acoustic scale that is assumed to take place in the perception of sound by humans. The SSI is a 2-D representation of sound with dimensions of ‘auditory filter frequency on a quasi-logarithmic (ERB) axis’ and ‘time-interval within the glottal cycle on a logarithmic time-interval axis.’ The SSI can be summarized by its spectral profile (Patterson et al. 2007), and the profile has the same scale-shift covariance properties as the SSI itself. They are like excitation patterns (Glasberg and Moore 1990), or auditory spectra.
Figure 1 shows that the distribution associated with the vowel /i/ shifts along the axis with acoustic scale. Thus, the transformations performed by the auditory system produce segregation of the complementary features of speech sounds, that is, the information about the size of the speaker, and the size invariant properties of speech sounds, like vowel type. In this way the transformations simulate the neural processing of size information in speech by humans. Experiments show that speaker size discrimination and vowel recognition performance are related; when discrimination performance is good, vowel recognition performance is good (Smith et al., 2005). This suggests that recognition and size estimation take place simultaneously. It is assumed that the acoustic scale information is essentially VTL information, and that it is used to evaluate speaker-size, and that the normalized shape information facilitates speech recognition and makes the recognition processing robust.
An HMM based syllable recognition system which is largely invariant to speaker size has previously been described (Monaghan et al., 2008). This recognition system relies on the size covariant representation of speech produced by AIM. Rather than discarding the size information, as this system does, we can use it to produce a system that simultaneously extracts speaker size and vowel type.
AIM is used in this study to pre-process input sound and facilitate the production of a low-dimensional feature vector for subsequent vowel identification and speaker size estimation. The feature vectors are expected to vary predictably with speaker size. A vowel pre-classifier is used to segregate recordings into their vowel types. These vowel-classified recordings are then passed to a vowel-dependent, statistical tool that estimates vocal tract length.
Methods, Assumptions, Procedures
To create the databases used in the experiments, a recording was made of a reference speaker speaking each of the five vowels: /a/ (as in ‘fa’), /e/ (as in ‘re’), /i/ (as in ‘mi’), /o/ (as in ‘do’), /u/ (as in ‘tofu’). The vocoder STRAIGHT was then used to scale these vowel recordings to a range of GPR and VTL values. STRAIGHT uses the classical source-filter theory of speech (Dudley 1939) to segregate GPR information from the spectral-envelope information associated with the shape and length of the vocal tract. STRAIGHT produces a pitch-independent spectral envelope that accurately tracks the motion of the vocal tract throughout the utterance. Subsequently, the utterance can be resynthesized with arbitrary changes in GPR and VTL.
AIM Feature Vector Extraction
SSI profiles, as described in section 1.1, were produced for 10-ms frames of each syllable file in the scaled syllable corpus. The profiles were produced using AIM-C, an implementation of AIM coded in C++ to accelerate the processing. Feature vectors were produced by first applying power-law compression with an exponent of 0.8 to the profile magnitude and, then, normalizing them to sum to unity. The profiles were treated like probability density functions and a modified version of the expectation-maximization (EM) algorithm described by Dempster, Laird and Rubin (1977) was used to fit a mixture of four Gaussians to the profiles. The parameters of this mixture of Gaussians make up the components of the low-dimensional feature vectors. The motivation for this technique can be understood by looking at the fit to the vowel /i/ shown in Figure 2. There are three main concentrations of energy in vowels and sonorant consonants and they have a roughly Gaussian shape. These are encoded by three of the Gaussians; the remaining Gaussian encodes a gap in the spectrum between the first and second formants.
To get a more consistent fit, the EM algorithm was modified in three ways: (1) the variance of the Gaussian was not updated but remained fixed at 115 channels squared, (2) the conditional probabilities of the mixture components in each filterbank channel were expanded according to a power-law (with an exponent of 0.6) and re-normalized in each iteration to reduce the overlap between Gaussians, and (3) an initialization step was introduced. Having a fixed variance reduces the number of degrees of freedom, resulting in a more consistent fit. The optimal value of the variance was

established during preliminary experiments using only the vowels. An additional justification for fixing the variance is that formants have roughly equal width on a log-frequency axis. Having wide Gaussians was found to prevent the fitting of Gaussians to individual resolved harmonics, reducing sensitivity to pitch variation. The initialization step fits two Gaussians to the profile, and uses the interval between the means of these Gaussians to provide an initial position for the four Gaussians in the second stage.
In previous automatic speech recognition (ASR) experiments (Monaghan et al. 2008), the AIM feature vectors just comprised the weights of the four Gaussians, which since they sum to one can be summarized as three parameters. When linear combinations of the differences in the means were added, the recognition rate increased slightly, but this was not considered sufficient to justify the increased dimensionality of the feature vector.
The VTL estimation stage requires feature vectors that vary in a predictable way with changes in VTL. If the excitations shift linearly on the ERB scale (as described in Section 1) and the EM algorithm gives a consistent fit for vowels, the means should be sufficient to characterize the shift and produce a VTL estimate. However, including the weights as well as the means should reduce the effect of any deviation from this model. The parameters of the Gaussians were collected for each frame in the fitting stage, and two sets of feature vectors were produced: one set for the recognition and refinement stage, and one for the VTL estimation stage. These feature vectors were assembled from combinations of Gaussian parameters found to be optimal for their separate purposes.
Producing Vowel Recognisers Using Mixtures of Multivariate Gaussians
Initial experiments were performed to ascertain the distinctness of the vowel clusters produced with two forms of feature vectors; one had just the three Gaussians weights, the other had the three weights and the three Gaussian mean differences. More distinct clusters mean that their probability density functions overlap to a lesser extent in the feature space, and so the probability of confusion between vowels will be lower. The distinctness of clustering was determined by calculating the average Kullback-Leibler (KL) divergence between vowels. For continuous distributions and , the divergence from to is defined as where the components of are the variables on which the distributions depend and the integral extends over the entire range for which and are defined. This definition is asymmetric in the sense that . Following a widely adopted convention, the average of the two divergences between each pair of vowels was used. On average, the KL divergences were found to be greater by three orders of magnitude when the differences between means are included. This indicates that feature vectors which include differences between means will give better vowel recognition than feature vectors which only contain weights.
The recognition stage employs five probability density functions (PDFs), one for each vowel. Multivariate Gaussian mixture models (MV-GMMs) provide the functional form for these PDFs. MV-GMMs consist of a linear sum of N, n-dimensional Gaussians; where n is the number of components in the feature vector. For each vowel these PDFs were obtained by taking the training data set, consisting of feature vectors known to correspond to the vowel, and, having chosen a value for N, using the standard EM algorithm to find the parameters of the Gaussians which provide the best fit to the data set. In the testing stage, a feature vector is input into each of these PDFs in turn, and the PDFs return a probability density. A hard vowel recogniser can be used which merely assigns the frame under question, an identity corresponding to the PDF which outputs the largest value of probability density. This system is inflexible and reduces the information available to the user, so it is preferable to have a soft recognition system which outputs a probability that a feature vector is a representation of each of the five vowels.
Spectral envelope ratio (SER) was used as a measure of VTL change in the recognition experiments. It is defined as SER = originalVTL/newVTL. The vowels were scaled from in SER from 0.75 to 1.25 (0.80 to 1.33 times the original VTL), keeping the original value of GPR. They were also scaled in GPR from 0.76 to 1.24 times, keeping the VTL constant at an SER value of 1. Initial experiments were performed using hard recognition, to establish optimum parameters. These showed that for both GPR and SER scalings, increasing the value of N does not have a significant effect on recognition performance. There were variations in performance for individual vowels, and occasionally changing N produced a substantial change, but there was no obvious pattern in the variation. Given these results, and in the desire to making the recogniser as economical as possible, N was fixed at two for all subsequent experiments. It was also found, as expected, that a six dimensional feature vector, consisting of weights and differences between means, gave better recognition performance over all the vowels than one consisting of just the weights (see Table 1).
Recognition performance is significantly better than chance for all vowels, for both GPR and SER scalings of the vowels, and with either three or six component feature vectors.
| Average Recognition Success: GPR Scaling | Average Recognition Success: SER Scaling | |
|---|---|---|
| 3 Component Feature Vectors | 88.6% | 80.4% |
| 6 Component Feature Vectors | 94.3% | 82.4% |
Energy and probability density thresholds
A soft recognition system was created by dividing the probability density output from each of the five vowel recognisers by a normalisation factor. The normalisation factor was simply the sum of the probability densities output by each vowel recogniser. This soft recognition system produces a vector of five values, one for each vowel, expressing the probability that the current frame is that vowel. The vowel with the largest probability is the candidate for that frame. This approach assumes that the phoneme in the frame is a vowel, and two criteria were introduced to remove frames containing consonants and/or noise. Firstly a low-limit energy threshold removed frames containing background noise and as well as some plosive and fricative consonants. A second threshold was then imposed on the probability density normalisation factor; frames with normalisation values less than the threshold value were assumed to be consonants or noise, and the soft recognition probabilities for all vowels were set to zero for these frames. Although this reduced the total number of frames available for VTL estimation considerably, the rate of vowel frames is, nevertheless, ample for VTL tracking, and the database that the system produces is restricted to the more valuable frames.
VTL Estimation using Minimum Mean Squared Error Regression
Database and training range
It is important to know how dependent the estimation system is on the training set used. Accordingly, STRAIGHT was used to produce a large number of combinations of VTL and GPR as the corpus for training and testing (see Figure 5). There were three training sets: T0 was a set densely sampled in VTL but extending only over a central region, T1 was a sparsely sampled set varying in VTL only but extending to extreme values, and T2 was a densely sampled set varying in both VTL and GPR around a central region.
VTL Estimators
Five VTL estimators were created, one for each vowel; it is assumed that the input has already been classified as a vowel. Each VTL estimator incorporates a GMM of the probability density of the feature vectors, trained using the standard EM algorithm. The feature vectors used to train the GMM contain the VTL of the source. Three different feature vectors were investigated: one consisting of just the four means and the VTL; one with four means, three weights and VTL; one with four means, three weights, VTL and GPR. In the testing stage, the GMM acts as the estimator in a minimum mean square error (MMSE) procedure; given the values of the components of a feature vector minus the VTL, the estimator calculates a VTL value such that the mean square error is minimised.
The GMM may be produced with a variable number, N, of Gaussian components, and the usual constraints apply to the choice of N. When N is small, increasing it often leads to better fitting distributions, and thus to more reliable VTL estimation. However, increasing N to excessively high values can result in over-training of the estimators with too many Gaussians used to fit minor details of the data that are specific to the training set, and this reduces the applicability of the final estimator. The value of N should also be minimized inasmuch as computational load grows non-linearly with N – in both the training and testing stages. An optimum value of N was sought given these considerations, and the assumption that N can be optimised independently of other parameters. The optimal value of N was found to be four and so this was used in all subsequent experiments.
In addition to the energy and normalisation criteria, one further refinement stage was added to the VTL estimation stage. Before a frame was accepted for VTL estimation, the value of the vowel identification probability was required to exceed a criterion value. The motivation for this step was the assumption that frames for which the probability of recognition is low, will give a less accurate VTL estimate. The effect of applying this refinement is evident in the clustering that occurs in the space of the Gaussian means (see Figure 6). The upper panel shows the data without the refinement; for each of the vowels, there are a substantial number of frames that fall away from the main cluster (chiefly to the right of the cluster). As the refinement criterion is increased, the procedure removes many of the frames which lie far from the vowel clusters, as illustrated in the lower panel, while removing only a few from the main clusters.
Results and Discussion
Vowel identification
Vowel recognition
The results in this subsection are for feature vectors containing the three Gaussian weights, and the mean differences between the first Gaussian, on the one hand, and the second, third and fourth Gaussians, on the other hand. By far the most important factor for recognition performance is whether the frame is presented to its own vowel recogniser, or one of the other vowel recognizers. In the latter case, the probabilities are so low as to be completely rejected. Accordingly, the discussion of the results is limited to cases where the frame is presented to the appropriate recognizer.
Recognition performance for vowels scaled in GPR and VTL is shown in Figure 7 and Figure 8, respectively. The probability is invariably high within the training region and regions immediately adjacent to the training region, indicating that the train and test system is working properly. Figure 7 shows that performance is essentially independent of GPR in the region below the training region for all vowels and performance drops off only slowly in the region above the training region. The pattern of performance is similar for all five vowels.
Figure 8 shows that performance drops off as VTL decreases below the training region and the rate differs a little between the vowels. As VTL increases in the region above the training region, performance drops off more slowly and the region of correct generalization is about the same size for all five vowels. Together the results show that the system can recognize the vowels reliably.
Soft Classification of syllables
The ability of the soft recognition procedure (described in section 2.2.1) to differentiate between vowels and consonants was tested. The testing procedure consisted of analysing six different syllables (“ar”, “et”, “lo”, “si”, “up”, “va”) spoken by the reference speaker. These were chosen to reflect the variety of syllabic communication sounds: together these syllables include all five vowels with sonorants (“ar”, “lo”), fricatives (“si”, “va”) and stops (“et”, “up”). Initially the identification was attempted with no constraints (see Figure 9). The vertical dashed turquoise lines divide the vowel from the consonants in each syllable; the division points were estimated from the waveforms of the sounds.
For the majority of frames in the vowel region of each syllable, one vowel is correctly identified as being much more probable than the others, giving the plateaus at probabilities of one. These plateaus exist for the consonant part of the syllable as well indicating that, in their current form, the recognisers will misidentify consonants as vowels. To overcome this problem a normalisation criterion of was chosen, and probabilities for all frames corresponding to un-normalised spectral profiles with log-energies below -2.5 were set to zero. The recognition probabilities with this refinement are presented in Figure 10.
The consonant activity in these syllables has been entirely removed and the only syllable exhibiting partial misidentification of the vowel is “si”, and even here the majority of frames in the vowel segment were correctly identified. These results are very promising overall and indicate that the recognition stage of the estimator works well.
Vocal tract length estimation
The previous subsection demonstrated that vowel frames can be correctly identified by the recognition stage. This subsection shows that the VTL estimator can produce accurate and consistent estimates of VTL for these pre-classified vowels. It then remains to demonstrate that these modules could be made to work together to estimate VTL, syllable-by-syllable from a stream of speech sounds.
VTL Estimation with Refined Feature Vectors
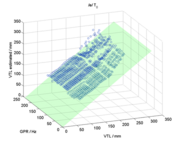
VTL estimates were produced for every frame of every vowel identified by the recognizer, in all of its scaled forms, separately for the three- and six-component feature vectors, and separately for each of the training sets described in section 2.3.1. The values were then averaged over frames within each vowel token, and this is the basic datum for the results. Figure 11 shows the results for the estimator trained on T0, with feature vectors consisting of VTL, three weights and four means. The green plane shows the true value of VTL; the VTL estimates lie on or just above the plane throughout its length and breadth. The figure shows the results for tokens of the vowel /e/; the pattern of results was similar for the other vowels in the study.
The performance of the VTL estimator was evaluated by calculating the percentage of VTL estimates which fell within a criterion range about the ‘true VTL’ plane. The criterion was set using the just noticeable difference (JND) for human discrimination of VTL, which Smith et al. (2005) estimated to be 9%, on average, for isolated vowels. The level of performance for the condition shown in Figure 11 is 88.4%. The form of the deviation is shown in Figure 12 which is a projection of the data in Figure 11 onto the VTL-VTLest plane. Estimated VTL drifts up slowly from the true value in the region where true VTL is considerably greater than that presented by the training set. This implies that there is some deviation from linearity in the shifts of the pattern in the SSI associated with the larger changes in VTL; without training data in these regions, the estimator cannot maintain its accuracy. One possible source of non-linearity is the fact that the ERB scale is not precisely logarithmic. The difference between a pure logarithmic scale and the ERB scale is greatest at the low-frequency end. As VTL increases, the formants are shifted lower in frequency, with the result that, for these values, the predictions are more affected by the non-logarithmic nature of the scale. The estimator will therefore overestimate VTL in this region.
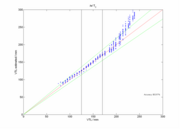
The range of VTL is much greater in T1 and the performance of the VTL estimator is considerably better for T1; when the feature vector has the same make up (i.e., both Gaussian weights and means), performance rises from 88.4% to 94.4%. Figure 13 shows the corresponding projection of VTL performance onto the VTL-VTLest plane when the training set is T1; it shows that the deviation is reduced considerably at the higher VTL values, as would be expected.
The performance values for all three of the individual training sets are presented separately for the different feature vectors in Table 2. There are the same number of tokens in T0 and T1, so the superiority of T1 is very likely due to the greater variation of VTL in T1. It is to be noted, however, that even with the restricted range of VTL values in T0, performance degrades only gradually in the region above the training data (Figure 12).
Performance with T2, which has a degree of GPR variation, is effectively the same as with T0, indicating that including GPR variation does not improve performance, even when GPR was added to the feature vector. This suggests either that the system is robust to GPR variations, or that GPR variation produces unpredictable changes in the profile that the system cannot be trained to account for.
| Training set | T0 | T1 | T2 |
|---|---|---|---|
| Four means and three weights | 85.2% | 92.0% | 86.3% |
| Four means alone | 88.4% | 94.4% | 87.2% |
| Four means, three weights and GPR | - | - | 86.5% |
Table 2: Percentage of correct VTL estimates for each feature vector and training set, averaged over vowel type. VTL estimates were judged to be correct if they fell within 9% of the true VTL.
Conclusions
Using AIM as a pre-processor, a procedure was developed for distinguishing between the vowel and consonant parts of syllables, and for identifying the vowel. A VTL estimator was also created which operated on the pre-identified vowel frames. Working in series, these routines can be used as a system for estimating VTL on a frame-by-frame basis from a stream of speech. Performance at the recognition stage was high overall, but declined at extreme values of VTL. Feature vectors composed of weights and differences between means gave higher percentage recognition success than those composed of weights only. GPR variation had a much smaller effect on performance than VTL variation. The ability of the recognizer to distinguish between vowels and consonants was very promising; all of the example syllables were correctly segregated. In contrast to existing ASR techniques, this report is founded on work that at each level aims to model the human system. When the estimator was limited to a central training range, it was able to emulate the robustness of HSR into VTL regions beyond everyday experience. Estimation performance was largely unaffected by GPR variation. The study provides proof of concept for VTL estimation based on AIM feature vectors.
Acknowledgements
The research was supported by the UK Medical Research Council (G0500221; G9900369) and by the Air Force Office of Scientific Research, Air Force Material Command, USAF, under grant number FA8655-05-1-3043. The U.S. Government is authorized to reproduce and distribute reprints for Government purpose notwithstanding any copyright notation thereon. The views and conclusions contained herein are those of the author and should not be interpreted as necessarily representing the official policies or endorsements, either expressed or implied, of the Air Force Office of Scientific Research or the U.S. Government.
References
Dempster, A. P., Laird, N. M., Rubin, D. B. (1997). Maximum Likelihood from Incomplete Data via the EM Algorithm, Journal of the Royal Statistical Society. Series B (Methodological), 39, 1-38
Fitch, W. T., and Giedd, J. (1999). “Morphology and development of the human vocal tract: A study using magnetic resonance imaging,” J. Acoust. Soc. Am. 106, 1511-1522.
Glasberg, B. R., Moore, B. C. J., (1990) Derivation of auditory filter shapes from notched-noise data. Hearing Research 47, 103-138.
Kawahara, H., Irino, T. (2005). Underlying principles of a high-quality, speech manipulation system STRAIGHT, and its application to speech segregation. In P. Divenyi (Ed.), Speech separation by humans and machines. Kluwer Academic: Massachusetts, 167-179.
Irino, T., Patterson, R. D. (2002). Segregating Information about Size and Shape of the Vocal Tract using the Stabilised Wavelet-Mellin Transform, Speech Communication, 36, 181-203.
Ives, D. T., Smith, D. R. R. and Patterson, R. D. (2005). "Discrimination of speaker size from syllable phrases," J. Acoust. Soc. Am. 118 (6), 3816-3822.
Monaghan, J.J.M., Feldbauer, C., Walters, T.C., Patterson, R.D. (2008) “Low-Dimensional, Auditory Feature Vectors that Improve VTL Normalization in Automatic Speech Recognition”. Acoustics’08 Paris
Patterson, R.D., Smith, D.R. R., van Dinther, R., and Walters, T. C. (2006). Size Information in the Production and Perception of Communication Sounds. In W. A. Yost, A. N. Popper and R. R. Fay (Eds.), Auditory Perception of Sound Sources. Springer US, 43-75
Patterson, R. D., van Dinther, R. and Irino, T. (2007). “The robustness of bio-acoustic communication and the role of normalization,” Proc. 19th International Congress on Acoustics, Madrid, Sept, ppa-07-011.
Smith, D.R.R., Patterson, R.D., Turner, R., Kawahara, H., Irino, T. (2005). The processing and perception of size information in speech sounds. Journal of the Acoustical Society of America, 117, 305-318.