PGWshar10.3
From CNBH Acoustic Scale Wiki
Roy Patterson , Etienne Gaudrain, Tom Walters
Contents |
3. The Pulse-Resonance Tones of Musical Instruments
This section describes how the sustained-tone instruments of the orchestra produce their tones, and the relationship between the physical properties of the instrument on the one hand, and the three main acoustic properties of these sounds on the other hand.
3.1 The Source of Excitation and the Acoustic Scale Variable, Ss
In general terms, the ‘source’ in these instruments is a highly nonlinear, resonant system that produces a temporally-regular stream of acoustic pulses. The mechanism is conceptually similar for the voice, brass instruments and woodwind instruments; in these instruments, the source momentarily interrupts the flow of air from the lungs, and it does so regularly in time. The individual mechanisms are, however, quite diverse. For example, the source is the vocal folds in the case of the voice; whereas, in brass instruments, it is the lips coupled to the main tube via the mouth piece; and in the woodwinds it is the lips coupled to the main tube via the reed. In string instruments, the mechanism is completely different; it is the bow coupled to a string. Despite the diversity of mechanisms, all of the sources produce streams of very precise acoustic pulses (brass and woodwinds), or abrupt changes in amplitude (strings) that function in a similar way. As a result, the sound waves produced by sustained-tone instruments are all pulse-resonance sounds. (In Fourier terms, the overtones of the pulse rate are locked to the pulse times both in frequency and phase up to fairly high harmonic numbers.)
The acoustic scale of the source of excitation is termed the source scale or Ss; it is effectively the repetition rate of the wave as it occurs in the air between the instrument and the listener. Ss is determined by physical properties of the instrument, like length and mass, which are not themselves acoustic variables. Ss largely determines the pitch we hear, but Ss is not itself an auditory variable. It is an intervening, acoustic variable that describes a property of the sound in the air, and it should be distinguished from pitch which is the auditory variable of perception. The relationship between Ss and the physical variables of the instrument will be illustrated by comparing how Ss is determined in the vocal tract and in string instruments.
3.1.1 The Source of Excitation in the Human Voice
The vocal folds produce glottal pulses in bursts and, although the vocal folds are rather complicated structures, the effect of the physical variables on the rate of pulses can be described using the expression for a tense string. The glottal pulse rate, GPR, is largely determined by the length, L, mass, M, and tension, T, of the vocal folds, and the form of the relationship is
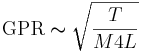 (1)
(1)
Two of these physical variables are determined by the size of the person – the length and mass of the vocal folds. Both of these variables increase as a child grows up, and both of these terms are in the denominator on the right-hand side of the equation, so as the child increases in height the pitch of the voice decreases. The average GPR for small children is about 260 cps, both for males and females. For females GPR just decreases with height throughout life dropping to, on average, about 160 cps in adult women. For males, GPR decreases with height until puberty at which point the vocal folds suddenly increase in mass and the GPR drops to, on average, about 120 cps in men. So the length and mass of the vocal folds are a major determinant of vocal register, that is, whether a singer is a soprano, alto, tenor, baritone or bass.
To produce a melody, a singer varies the tension of his or her vocal folds. So learning to sing in tune is largely a matter of learning to control the tension of the vocal folds — holding the tension fixed during sustained notes and changing it abruptly between notes. Tension is in the numerator of the mathematical expression (1), and so as a singer increases the tension, he or she increases the GPR. There is considerable overlap in the note ranges of the soprano, alto, tenor, baritone and bass voices; in fact, the highest note of a bass is typically a note or two above the lowest note of a soprano. The effect of all three of these variables (T, M, and L) on GPR is constrained by the fact that the GPR value is related to the square root of these variables. So, for example, a singer has to change the tension of the voice by a factor of four to produce a one octave change that would double the GPR.
In summary, for a specific individual, the size of the vocal folds (length and mass) determines the individual’s long-term average GPR, and it determines the Ss component of the register of their voice. The tension of the vocal folds is varied to produce a melody. So, the long-term average Ss value, calculated over a sequence of musical phrases, reveals the register of the singer’s voice; short-term deviations of Ss from the longer-term average, in discrete steps with regular timing, are the hallmarks of vocal melody.
3.1.2 The Source of Excitation in the String Family
The excitation mechanism in stringed instruments is the string pushed by the bow. As the musician draws the bow across a string, the string is pushed or pulled away from its resting position until the tension becomes too great, at which point, it snaps back, producing an abrupt, uni-directional change in amplitude. The direction is opposite to the direction that the bow is moving. The result is, nevertheless, a pulse-resonance sound inasmuch as the harmonics are locked in phase, and the internal representation of the sound has a pulse-resonance form in any given frequency band. Although the bow-string system is rather complicated physically (McIntyre et al. 1983), the relationship between pulse rate, PR, and the main physical variables is the same as for the vocal folds, namely,
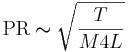 (2)
(2)
In this case, however, T, M, and L refer to the tension, mass and length of the string, rather than to the corresponding properties of the vocal folds. The two physical variables associated with the size of the source (the length and mass of the string) are the most important excitation variables in this family of instruments and they each have two roles to play. Consider first the pulse rates of the open-strings on these instruments: Both the mass and length variables are in the denominator on the right-hand side of the equation, so increases in size, be they length or mass, lead to decreases in pulse rate. For a given member of the family (violin, viola, cello or contra bass), the length of the four strings is fixed, and as the size of a family member increases, the string length gets longer in discrete steps. As a result, string length plays an important role in determining the register within the string family. The mass of the string increases with its length, so it also contributes to the register we perceive. Mass also plays an important role in determining the range of notes that an individual instrument can play; the mass is varied across the four strings to extend the range beyond that which can be provided on any one string. Finally, the musician varies the length of individual strings to produce the different tones within that string’s range.
Instrument makers are very adept at using mass and length to vary the pulse rate of notes within a family. If a musician depresses the lightest string on the largest instrument (the contra bass) at a point near the bridge on the neck, the pulse rate of the note will actually be a little higher than the pulse rate of the open-string note of the heaviest string on the smallest member of the family (the violin). In both cases, the notes are just below middle C on the keyboard.
3.1.3 Excitation Mechanisms of the Woodwind and Brass Instrument Families
The excitation of woodwind and brass instruments is described in terms of fluid mechanical ‘valves’ that momentarily close the flow of air through the instrument. The closure causes a sharp acoustic pulse which resonates in the tube beyond the mouthpiece. For woodwind instruments, the valve is the reed in conjunction with the lips. For brass instruments, the source is not clearly localised within the instrument. The source of energy is the stream of air produced by the player who controls the pressure with the tension of the lips. The source of excitation is pulsatile because the mouthpiece is coupled to the tube between the mouthpiece and the bell (i.e. the body of the instrument), and the tube can only resonate at certain frequencies. Thus, the pulses originate from the lips, but the pulse rate is determined by the effective length of the tube, and this functional tube length is varied by the valves (or the slide) to control the pulse rate of the note.
Despite the complexities of excitation, these two families of instruments produce pulse-resonance sounds in which the acoustic scale of the source Ss controls the repetition rate of the note, and thus contributes to define the instrument’s register within its family. The pulsatile nature of the excitation generated by these systems, and the temporal regularity of the pulse stream, mean that the dominant components of the spectrum are strictly harmonic and they are phase locked (Fletcher and Rossing 1998). Fletcher (1978) provides a mathematical basis for understanding the origin of the phase locking, which is referred to as mode locking in musical instrument theory. Detailed descriptions of the mechanisms are provided in Benade (1976), Fletcher (1978), and McIntyre et al. (1983); a brief overview is provided in van Dinther and Patterson (2006).
3.1.4 Summary of the Role of Ss in Determining Melody and Register Within a Family
Comparison of the excitation mechanisms for the different instrument families shows that these mechanisms are similar, inasmuch as they all produce regular streams of pulses and the pulse rate is affected in the same way by the size of the components in the source. As a result, pulse rate decreases as instrument size increases in all of these instrument families. At the same time, the method whereby the pulse rate is varied to produce a melody is fundamentally different: the variable that controls pulse rate in the voice is the tension of the vocal folds, and the singer increases the tension to increase the pulse rate; whereas the variable that controls pulse rate in string instruments is string length, and the musician decreases the length to increase the pulse rate. The brass and woodwind instruments are like the strings, inasmuch as the pulse rate is varied to produce a melody by varying the length of part of the instrument; brass and woodwind instruments are different from the strings inasmuch as the length in this case is tube length rather than string length.
Although different instrument families employ very different mechanisms to produce acoustic pulses (and it is important for musicians to understand something of these mechanisms in order to play their instruments properly), all of these instruments nevertheless produce pulse-resonance tones, and the melody information in music is a sequence of pulse-rate values that specify the momentary acoustic scale of the source of excitation. Although the relationship between the physical variables involved in instrument excitation and the repetition rate of a given note is complex, the relationship between the acoustic-scale variable, Ss, which summarizes the action of the source, and the pitch we perceive is straightforward.
3.2 The Filtering of the Excitation Pulses and the Acoustic Scale of the Filter, Sf
The ‘filter’ in musical instruments is a set of resonators that increase in size with register within an instrument family, and together the resonators determine the acoustic scale of the filter, Sf. Each of the pulses produced by the excitation mechanism of a sustained-tone instrument is filtered by body resonances within the instrument. In the time domain, it is these resonators in the body of the instrument that produce the resonances that appear attached to each pulse in the waveform (e.g., Fig. 1a). In the frequency domain (e.g., Fig. 1b), the body resonances produce the distinctive shape of the envelope of the magnitude spectrum, and consequently, they determine the timbre of the family. In the case of the voice, the dominant resonances are associated with the larger cavities of the vocal tract (Chiba and Kajiyama 1941; Fant 1960). The tongue makes a constriction in the vocal tract that divides it into a mouth cavity and a throat cavity. These cavities resonate like tubes and/or bottles and they introduce formant peaks into the vowel spectrum (Fig. 1b). The tongue position is varied to produce the different vowels. This changes the relative sizes of the cavities, and thus, the relative positions of the formants in the spectrum (Chiba and Kajiyama 1941; Fant 1960). For stringed instruments, the most important resonances are associated with the plates of the body (wood resonances), the body cavities (air resonances), and the bridge (structural resonances) (Benade 1976). For brass and woodwind instruments, the prominent resonances are associated with the shape of the mouthpiece, which acts like a Helmholtz resonator, and the shape of the bell which determines the efficiency with which the spectral components radiate into the air (Benade and Lutgen 1988). Woodwind instruments are like brass instruments, but the materials are different. So, just as there are many source mechanisms for generating the pulse stream, there are many systems of body resonances which lead in turn to many distinctive spectral envelopes.
Within a family of instruments, the most prominent distinction between the members of the family is the size of the body of the instrument, and the primary effect of instrument size on the perception of register within a family is straightforward (van Dinther and Patterson 2008): If the size of an instrument is changed while keeping its shape the same, the result is a proportionate change in Sf, the acoustic scale of the filter mechanism in the body of the instrument. That is, if the three spatial dimensions of an instrument are increased by a factor, a, keeping the materials of the instrument the same, the natural resonances decrease in frequency by a factor of 1/a. The shape of the spectral envelope is preserved under this transformation, and so, if the spectral envelope is plotted on a log-frequency axis, the envelope shifts as a unit towards the origin, without changing shape, and the change in Sf will be the logarithm of the relative size of the two instruments: log(1/a). This uniform scaling relationship is called ‘the general law of similarity of acoustic systems’ (Fletcher and Rossing 1998), and it is used to produce much of the difference in Sf between the tones produced by different instruments within a family. Numerical examples illustrating how the spatial dimensions of an instrument affect its resonances are provided by van Dinther and Patterson (2006).
Comparison of the filter systems of the different instrument families shows that the spectral envelope is affected in the same way by changes in the size of the filter-system components; specifically, the resonant frequencies decrease as body size increases and so the spectral envelope shifts towards the origin as the sizes of the components increase. So size affects the filter system in the same way as it affects the excitation mechanism. It is another example of the fact that bigger things vibrate more slowly. The wood-plate and bridge resonances of the string-family filter system are complex, and they are fundamentally different from the bell and mouthpiece resonances of the brass-family filter system, which are also complex. Despite the complexity of the relationship between the physical variables involved in body filtering and the shape of the resultant spectral envelope, the relationship between the acoustic properties and the perception of the notes is fairly straightforward. The shape of the spectral envelope determines the family aspect of timbre; the acoustic scale of the filter, Sf, determines the register we perceive, and thus, which instrument within the family. In all of these instrument families, the register decreases from soprano to bass as instrument size increases and the spectral envelope shifts toward the origin.
3.3 Constraints on the Acoustic-Scale Variables in Orchestral Instruments
In sections 3.1 and 3.2, the relationship between the physical variables involved in the production of musical tones, and the acoustic scale of the source, Ss, and the filter, Sf, was presented in theoretical terms without reference to the practicalities of constructing and playing instruments. In the real world, it turns out that it is not possible to simply scale the spatial dimensions of instruments to achieve registers ranging from soprano to bass in most instrument families; the bass member would be too large and/or the soprano member too small. This section reviews the spatial scaling problem, and describes how the instrument makers produce tones with a wide range of acoustic scale values without using excessively large or small instruments.
The spatial scaling problem arises from the desire to simultaneously satisfy three design criteria for families of sustained-tone instruments: The first criterion is that the instruments should produce notes which are heard to have a strong musical pitch, whose clarity and salience provide for effortless communication of melodies and their variations. This places an important constraint on the relationship between the acoustic scale variables, Ss and Sf. The instrument’s filter system must resonate at frequencies corresponding to the first ten harmonics of the pulse rate of each note that the instrument is intended to play; that is, the instrument must emit significant amounts of acoustic energy in the range from the pulse rate of each note to three octaves above that pulse rate. This is necessary because the pitch of notes where the energy is carried by harmonics above about the tenth is not sufficiently salient to support accurate perception of novel melodies (Pressnitzer et al. 2001; Krumbholz et al. 2000). The second criterion is that the members of each instrument family should, together, produce notes that cover a significant portion of the musical scale, which for the keyboard encompasses about seven-octaves from, say, 27.5-3520 cps. When combined with the first criterion, the second criterion effectively requires that the instruments of a given family have matched Ss and Sf values for all of the registers in the range from soprano to bass. This is a very demanding constraint, particularly when combined with the third criterion, which is that the instruments should be playable and portable. This last, practical constraint places limitations on the sizes of instruments which, in turn, means that the desired range of notes cannot be achieved by simply scaling instrument size in accordance with the law of acoustic similarity.
There are problems for the instrument maker at both ends of the register range. For example, in the string family, there is a limit to how short the neck can be on the smallest member of the family (the violin) if the contact points where the string is pressed onto the neck are to be far enough apart for a musician to play the notes of a melody accurately and quickly. And at the other end of the range, if the instrument maker attempts to scale up the soprano version of the family to provide the bass member, the instruments become too large to play and too large to carry. Hutchins (1967, 1980) described the problems encountered when you try to construct a family of eight stringed instruments covering the entire range of orchestral registers based on the properties of the violin. The double bass member of the family would have to be six times the size of the violin, if simple scaling of instrument dimensions were to be used to provide a shift of six octaves in the spectral envelope. The length of a violin is about 0.6 meters, so the double bass in this hypothetical family would have to be 3.6 meters tall. The lower notes on the strings of such a double bass would not be reachable for most musicians and the instrument would not be portable. So, the problem is this: Although instrument makers can scale the dimensions of instruments to achieve much of the desired change in Ss and Sf, it is not possible to use the scaling of spatial dimensions, on its own, to provide the full range of registers in each family, and at the same time, ensure that the pitch of each note is sufficiently strong to support accurate melody perception.
So how do instrument makers solve this problem, and how do they construct families of instruments that produce tones with salient pitches over the full range of registers from soprano to bass – instruments which are, at the same time, playable and portable? The first criterion of instrument production is immutable; the instrument must produce energy in the first three octaves of the pulse rate if the note is to have a well defined pitch. The third criterion is essential; the instruments have to be playable and portable. So how do the instrument makers provide a wide range of notes on instruments with manageable sizes? This is where the knowledge and craft of the instrument maker come to the fore. What is required is not that the soprano instruments be excessively small and the bass instruments be excessively large; what matters is that the instruments produce tones with a wide range of Ss and Sf values, and that the Ss and Sf values are coordinated throughout the range. So what the instrument makers have done is find ways of extending the range of Ss and Sf values beyond what is practical with spatial-dimension scaling, by adjusting other physical properties of the instruments such as the mass of the strings, the thickness of the plates or the depth of the volume of the air cavity. They scale the physical dimensions of the family so that the largest member is portable and the smallest member is playable, and then they adjust other physical properties of the instrument to achieve the desired acoustic scale values for the source mechanism and the filter system (e.g. Schelleng 1963).
Consider the case of the source scale in the string family: The strings on the larger members like the cello and contra bass are not as long as the law of acoustic similarity would require because it would make the instruments unwieldy. The instrument makers increase the linear mass of the strings (the mass per meter) by winding metal coils around the string. This increased mass causes the strings to vibrate more slowly as illustrated by equation 2. The instrument makers use a change in mass to obtain the lower ranges of notes on the lower strings of any given member of the family.
With regard to the filter scale in the string family: The filter systems of the larger members of the family are not as large as the law of acoustic similarity would require, because it would make the instruments too heavy and too large. The instrument makers adapt the characteristics of the instruments to preserve the sound quality while making them usable at the same time. The main resonance is driven by the cavity mode of the body which functions like a Helmoltz resonator. The volume of the instrument as well as the surface area of the f-holes are the key parameters. The open strings of the cello are tuned to pulse rates three times lower than those of the violin. However, the plates of the cello’s body are only 2.1 times larger than those of the violin (Schelleng 1963), while the rib height of the cello is about four times that of the violin (Fletcher and Rossing 1998). Thus the volume of the cello is 17 times larger than that of the violin; this is equivalent to uniform spatial scaling by a factor of 2.6. To lower the body resonances to the desired values, the instrument makers vary the mass, thickness and arching of the body plates. Specifically, the body plate of the cello is made proportionally thinner than that of the violin which lowers the body resonance frequency (e.g. Molin et al. 1988).
Having established that the acoustic scale variables are balanced in the sustained-tone instruments of the orchestra, we can return to the secondary aspect of register, associated with the perception of tones from a single instrument, i.e. the within-instrument register. Register, in this sense, is ‘a part of an [instrument’s range] having a distinctive tonal quality’ (Kennedy 1985, p. 585). So we speak of the chest and head registers of an individual’s voice, or the upper and lower register of an instrument’s range. In acoustic scale terms, the perception of register within an instrument’s range, is a perceptual distinction concerning the relative values of Ss and Sf. When the Ss values of a succession of notes are high relative to the Sf of the singer or the instrument, we perceive that the person is singing, or the instrument is playing, in the upper register, and vice verse.
Finally, note that that the range of tones covered by the registers of the voice, from soprano to bass, is only about four octaves in total (from about C6 down to a little over C2). The range of the string-family instruments (taken together) covers almost seven octaves (from just under C8 to just over C1). The singing teacher can help a vocalist strengthen tones towards the ends of their natural range, but they cannot stretch the vocal tract length or add significant mass to the vocal folds.
In summary:
1. Although the physics of the source mechanisms that excite the sustained-tone instruments are complicated, and they vary markedly from family to family, the acoustic scale of the source, Ss, provides a convenient summary of the action of the source as it pertains to tone perception. The source determines the repetition rate of the wave, or the position of the fine structure of the magnitude spectrum (on a log frequency axis), and this, in turn, determines the pitch of the tone, and contributes to the perception of an instrument’s register within its family.
2. Although the physics of the resonance mechanisms that filter the source waves are complicated, and they vary markedly from family to family, the acoustic scale of the filter, Sf, provides a convenient summary of the action of the filter with regard to its contribution to the perception of an instrument’s register within its family.
3. Within a family, when source size is increased to increase the acoustic scale of the tones and lower the pitch, the acoustic scale of the filter has to be increased to maintain the distinctive timbre of the family, and to ensure that the tones continue to produce a strong pitch. At the same time, the increase in filter scale contributes to the lowering of the perception of the register of the instrument within its family.
4. Within a family, it is not possible to produce tones whose pitches span the entire range of the keyboard simply by varying the spatial dimensions of the source and the filter. To achieve the desired acoustic scale values, and the appropriate balance between the acoustic scale values, the instrument maker has to vary other physical properties like the mass of the strings and the stiffness of the plates.
