The Space of Auditory Perception

From CNBH Acoustic Scale Wiki

Jump to: navigation, search
← Category:Introduction to Communication Sounds
Crystal Clear action configure.png

This page is currently under construction.
You can check the latest changes in the history.

In the auditory image model of perception, it is argued that the cochlea and midbrain together construct the auditory image in a {linear-time, log2(cycles), log2(scale)} space. Briefly, the basilar membrane performs a wavelet transform which creates the acoustic scale dimension of the auditory image (the vertical dimension). It is the 'tonotopic' dimension of hearing and it is a close relative of the traditional frequency dimension but it is fundamentally logarithmic. The acoustic scale dimension is critical to auditory perception, but the basis of perception is not a simply a time-scale recording of basilar membrane motion (BMM). The inner hair cells and primary nerve fibres convert BMM into a two-dimensional pattern of peak-amplitude times, and it is this neural activity pattern (NAP) that flows up the auditory nerve to the brainstem, rather than the BMM itself. The NAP is a time-scale representation of the information in the sound that can be observed physiologically in the auditory nerve and cochlear nucleus, but the basis of perception cannot be the NAP itself.

Firstly, the duration of the NAP record in the auditory system is limited to about 5 ms, which is the time taken for neural signals to go from the cochlea to the inferior colliculus where the code changes and temporal integration occurs. Secondly, from the perspective of perception, there is information in the NAP that we do not hear, indicating that the basis of perception is a representation that is either in, or beyond, the inferior colliculus. Thirdly, to produce scale-shift covariance, a segment of time long enough to contain the resonances of communication sounds has to be converted to a cycles/scale representation. The auditory system exhibits scale-shift covariance for resonances up to 30 ms in durations, or more. The addition of the extra dimension and the form of the {cycles, scale} plane are described in Section 2.4.2 below. The addition of this third dimension provides a space that would appear to have the properties necessary to explain the robustness of auditory perception – a simulation of the auditory images we perceive in response to communication sounds. The category Perception of Communication Sounds contains a page on the details of the Space of Auditory Perception. It is an early version of The robustness of bio-acoustic communication and the role of normalization with the emphasis on perception rather than normalization.


Contents

The auditory wavelet transform and the {time, scale} NAP

The operation of the initial transform in the cochlea can be likened to a filterbank, in which filter centre frequency is distributed logarithmically with frequency and the bandwidth of the auditory filter is proportional to filter centre frequency. The envelope of the impulse response is a gamma function whose duration decreases as frequency increases. This means that, mathematically, the operation of the cochlea is more like a wavelet transform than a windowed Fourier transform, where the window duration is the same in all channels. This suggests that the auditory system is actually transforming the time waveform of sound into a {time, scale} representation, rather than a {time, frequency} representation. {Time,scale} versions of the four vowels in Fig. 1 are presented in Fig. 2.4.1. The activity in the four panels includes the operation of the hair cells and so it is intended to be a record of the NAP flowing from the cochlea up the auditory nerve to the brain stem in response to each of these sounds. By its nature, the time dimension in this representation is linear and the NAP exists in a {time, scale} space.

???’’’The NAPs in Fig. 2.4.1 were produced using the auditory filterbank module of AIM and a wavelet representation of the impulse response of the auditory filter to produce a BMM, which was then half-wave rectified to simulate transduction by the inner hair cell. The low-pass filtering that characterizes loss of phase locking has been omitted in this example to facilitate illustration of the properties of the space itself.] We need a way of marking what are like footnotes on things we want to reassure the reader we will deal with eventually should they be worrying about them, but without actually using footnotes. I think the traditional way to do it is with italics.’’’???

The right-hand ordinate of each panel is acoustic scale, and it is reciprocally related to acoustic frequency through the speed of sound; scale = (1/frequency)*velocity. So {time, scale} space is similar to {time, frequency} space; the right-hand ordinate is the more familiar variable, frequency, in log format. As a variable, however, scale has the advantage that it is more directly related to the wavelength of the sound, and thus, to the size of the resonators in the source. The unit of frequency is cycles per second and the unit of velocity is meters per second, so the unit of scale is meters per cycle. Thus, the NAP in a row of one of these panels is showing the individual cycles of the mechanical vibration produced by a resonator in the source, and the ordinate gives the scale of the cycle, that is, the number of meters per wavelength. This is directly related to the physical size of the resonator that produced this component of the sound, and since resonator size is typically correlated to body size, the {time, scale} NAP of a sound contains valuable information about the size of the source.

[The realization that the cochlea performs a wavelet analysis and produces a {time, scale} representation of the sound prompts the intriguing hypothesis that the cochlea may have evolved to enable animals to analyse the size information in sounds. This hypothesis is pursued in Section 3 below. The form of the auditory filter and the resulting {time, scale} representation that it produces are presented in Chapter XXX.]

[The {time, frequency} spectrogram does not show the cycles of the source; they are removed in the production of the magnitude variable of the spectrogram, and the variable, frequency, does not immediately prompt one to think in terms of source size. {Time, frequency} spectrograms of the four vowels in Fig. 1 are presented in Chapter XXX along with a discussion of the generalization-discrimination problems that arise when recognition is based on the features that arise in {time, frequency} space. The spectrogram destroys a portion of the scale information in the sound, whereas the wavelet transform preserves all of the scale information. It is argued that the process of segregating and tracking the different forms of information in communication sounds is hampered by the lack of scale information in spectrograms, and the fact that scale changes do not produce orthogonal changes in {time, frequency} space. This may well be one of the main reasons why the performance of computer recognition systems is so poor in natural environments.]

Although the {time, scale} representation of communication sounds is scale covariant, it is not scale-shift covariant. This is illustrated in Fig. 2.4.1 by the fact that a change in resonance size produces a change in the shape of the distribution, as well as its position in this time-scale space. The upper formant in each sound is a scaled version of the lower formant, but the representation of the upper formant is compressed in time with respect to the lower formant. Similarly, the distribution of activation expands in time, as a unit, when we switch from the smaller sources in the upper panels to the larger sources in the lower panels. This is the same effect in a different form. The scale information is preserved and it covaries with the dilation of the auditory figure in this {time, scale} representation. But the changes are not orthogonal; a change of acoustic scale in the sound produces a change along the time dimension of the figure as well as in the scale dimension. So, to repeat, the {time, scale} representation of communication sounds is scale covariant, but it is not scale-shift covariant. To solve this problem, a segment of the time-scale representation has to be transformed into a {log-cycles, log-scale} form as described in the next subsection, 2.4.2.

With regard to auditory processing, as noted above, the NAP cannot be the underlying neural representation that forms the basis of auditory perception. For research purposes, we often create extended {time, frequency} representations of the BMM and the NAP to show the details of the activity produced by a sound over the duration of a syllable (~200 ms) or so. And speech scientists create {time, frequency} spectrograms – an envelope representation with a reduced level of detail covering a complete utterance lasting for 2-3 seconds. It is important to realise, however, that BMM is essentially instantaneous and there is no record of BMM as such in the brain. The representation flowing up the auditory nerve is the NAP, and the duration of the segment of the NAP that exists in the brain at any given time is, at most, about 5 ms. This is the time required for a click response to progress to the cochlear nucleus and up through the superior olivary complex to the inferior colliculus, where the code for the information changes. This is indicated by the fact that the observed phase locking limit decreases from around 5000 Hz in the cochlear nucleus and superior olivary complex, down to more like 500 Hz in the inferior colliculus.

Finally, with regard to the representation in Figs 2.3 and 2.4.1, the wavelet transform used to produce these specific auditory images and NAPs was linear; that is, it did not include the compression of cochlea filtering. This wavelet is useful because the processing is transparent and the resulting NAPs present a clear view of the two damped resonances in the source. Chapter XXX describes a dynamic, compressive gammachirp auditory filterbank that includes the fast-acting compression observed at the interface of the passive and active components of the auditory filter. The compression alters the relative strength of the pulse and resonance in communication sounds. The pulse is typically large relative to the resonance in these sounds. So, although the pulse is very useful for marking the start of the message, it makes analysing the resonance difficult because the resonance is tucked in behind the pulse. Fast-acting compression within the auditory filter compresses the pulse amplitude with respect to the resonance amplitude and reduces the chance of the pulse masking the resonance. The value of this active compression is illustrated in Chapter XXX which details the dynamic compressive gammachirp auditory filter.


The cycles-scale operator and the instantaneous plane of the auditory image

To achieve scale-shift covariance, we need to expand time as scale decreases so that the unit of scale (one cycle) becomes the same size in each channel. This is accomplished simply by multiplying time as it exists in each channel of the NAP of a sound (e.g., the individual rows of the panels of Fig. 2.4.1) by the centre frequency of the channel in question. The unit of this new dimension is [cycles/second] X time, which reduces simply to cycles. This transformation is motivated by a consideration of the operators that can transform {time, scale} space into a scale-shift covariant space whose dimensions are log-cycles and log-scale (as in Fig. 2.3) – operators which are, at the same time, unitary. Such operators effect coordinate transformations that preserve physical properties like energy, and they have an inverse that enables transformation in the reverse direction. The expressions for the operator, S and its inverse, S-1 are:

(Sf)(\gamma,\sigma):=(\ln{2})2^{\frac{\gamma}{2}}f (2^{\gamma-\sigma},2^{\sigma}) \!

and

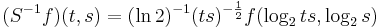(S^{-1}f)(t,s)=(\ln{2})^{-1}(ts)^{-\frac{1}{2}}f(\log_2{ts},\log_2{s}) \!,

where γ is log2(cycles), or log2c and σ is -log2(scale), or log2s. The operator indicates that if we use logarithmic scale units, then the shift of the neural pattern with a change in scale will be restricted to the vertical dimension; that is, it will be orthogonal to the cycles dimension. Similarly, if we use logarithmic cycle units, then the shift of the period-terminating diagonal with a change in pulse rate will also be restricted to the vertical dimension; that is, it too will be orthogonal to the cycles dimension. The expression in Eq. (9) says that the function, f, in time-scale space (on the right-hand side), is transformed into the function ‘Sf’ in {γ,σ} space by a particular exponentiation of time and scale. The normalization constant, , is required to make the transformation unitary. The important point for the current discussion is that this operator fixes the shape of the distribution of activation associated with the message of the sound, so that it no longer changes shape when either the pulse rate or the resonance rate change.

When the {time, scale} NAPs in Fig. 2.4.1 are transformed to {γ,σ} space, they appear as in Fig. 2.4.2. There are two striking differences between the NAPs as they appear in the new space and the more familiar {time, scale} space. Firstly, there is scale-shift covariance – the property that motivates the change of space. The activity in the first cycle of each NAP is essentially the same as that in the corresponding auditory image of Fig. 2.3. That is: (1) The pattern of activation that represents the message – the auditory figure – has a fixed form in all four panels; it does not vary in shape with changes in pulse rate or resonance rate. (2) When there is a change in resonance rate, the auditory figure just moves vertically, as a unit without deformation. (3) When there is a change in pulse rate, the auditory figure does not change shape and it does not move vertically; rather, the diagonal which marks the extent of the pulse period, moves vertically without changing either its shape or its angle. The other difference is that the second, third and fourth cycles of the sound are rotated by the time-to-cycles transformation, and compressed by the transformation from cycles to log2(cycles). The onset of the second cycle of the pattern defines the boundary of the auditory image; it is a positive diagonal (45 degree angle) and its position is defined by the scale of the pulse period, which is indicated by the point where the diagonal intersects the ordinate. The period in panel (c) is 32 ms, so σ is - 5. The start of the third cycle of activity is a parallel, positive diagonal that is shifted down by an octave, and so it would intersect the ordinate at – 4.

The rotation and progressive compression of the auditory figure in the second and third periods of the sound indicate that {γ,σ} space is not time-shift covariant. That is, successive copies of a sound have different forms. So the progression of auditory figures across this {γ,σ} NAP does not represent time as we perceive it in auditory perception. Auditory perception is time-shift covariant in the sense that we hear the same perception when a sound is played at two different times (separated by a reasonable gap). This suggests that the γ dimension is an extra dimension of auditory space, separate from time. We assume that the cycles dimension combines with the scale dimension of the NAP to create the {γ,σ} plane of auditory image space, in which the resonance information attached to the latest pulse of a communication sound appears as a scale-shift-covariant auditory figure. A brief description of a space, that has shift covariance for both forms of size information and time-shift covariance for events separated in time, is presented in the next subsection, 2.4.3, and this 3-D space is our model of auditory image space.

A detailed discussion of the {γ,σ} operator, the properties of the {γ,σ} space, and the relationship to some well known bilinear operators is presented in Appendix AAA. Whereas the {γ,σ} operator is strictly logarithmic, the scale dimension in the cochlea is quasi-logarithmic; the resolution of the auditory filter increases a little, in relative terms, as the centre frequency of the filter increases, and it the rate of increase is slower at the lowest centre frequencies (below about 500 Hz in humans). Appendix AAA includes an illustration of how the {γ,σ} operator can be modified to account for the fact that the place distribution in the cochlea is not precisely logarithmic.

Strobing and period-shift covariance: auditory image space

The flow of information in the auditory system, from the sound wave arriving at the ear canal, through the cochlea and up the auditory nerve to the auditory image is illustrated in Fig. 2.4.3. The diagonal dimension is time which is expanded to reveal the microscopic detail of the waveform and the NAP. This will be referred to as ‘physiological time’ to distinguish it from ‘psychological time,’ which is time as we experience it in auditory perception. Along the time line in the figure, a vowel sound proceeds towards the cochlea from the upper left, and each glottal pulse is followed by a copy of the vocal tract resonance. The cochlea converts the sound wave to a {time, scale} NAP; the vertical dimension is scale plotted on a logarithmic axis. The pulse produces a vertical structure in {time, scale} space and the cycles of the resonance follow it with the same temporal resolution as in the sound. The NAP is only one cycle in duration to remind us that there is only a very short segment of NAP in the auditory system at any one time. Indeed, in the example, it would have to be one cycle of a person with a relatively high pitch, 200 Hz, since there is only time for one 5-ms period between cochlea and inferior colliculus.

At the leading edge of the NAP, which represents ‘now’ in time, the information from the NAP flows out of NAP space, and across the {γ,σ} plane of the auditory image. Thus, the pulse is tied to γ = 0 and the tail of the resonance flows across towards the positive diagonal. The processing is controlled by the glottal pulses; that is, the processing is pitch synchronous and phase locked to the glottal pulses. A review of pitch synchronous analysis of speech and musical sounds is presented in Chapter XXX. As the peak of the NAP representation of a new glottal pulse is detected at ‘now’ in each channel, the transfer of information from the previous NAP period to the {γ,σ} plane ends abruptly on the period diagonal, and immediately restarts at γ = 0. This is referred to as ‘strobing’. The auditory images in Fig. 2.3 were produced in this way. We could model the operation of the {γ,σ} plane of the auditory image as a nearly-instantaneous process like the generation of the BMM and the NAP. In this case, each period of resonance information would create a separate auditory figure, and successive strobes would clear the {γ,σ} plane before commencing the construction of the next auditory figure. At the same time, the strobe would presumably cause a copy of the latest auditory figure to be sent on up the auditory system to serve as the basis for perception. However, this model of the information flow would not be a good model of auditory perception, inasmuch as the rate of glottal pulses in the voiced parts of speech is commonly in excess of 100 pulses per second, and we do not hear 100 separate auditory figures per second when listening to a sustained vowel; we hear a static perception.

To explain the stability of these perceptions, it is assumed that {γ,σ} plane has a short-term, exponential memory that integrates activity over time with a half life of about 30 ms; the resonance activity of the current NAP period is added to any activity that is already in the {γ,σ} plane. It is this time-averaged representation that is thought to best represent the auditory image that we perceive at time ‘now’ in response to a sound. The pulse period in communication sounds is typically short relative to the half life of the auditory image, 30 ms, and so the auditory figure of a pulse-resonance sound rises rapidly in place when the sound comes on. Since the image is refreshed frequently relative to the half life, auditory figures appear stable – fixed in position and level – until the sound changes. Despite the temporal integration, the auditory figure also decays rapidly when the sound goes off because 30 ms is still short with respect to our conscious experience of time. For computational convenience, since the cycles of pulse resonance sounds occur at a relatively high rate, we assume that the strobe reduces the activity in the {γ,σ} plane by the amount appropriate for the duration of the pulse period, at the end of the period, as the strobe is about to reset the γ dimension to 0. The generation of the auditory image from the NAP is like a multi-channel stroboscope which flashes each cycle of a rotating wheel to our visual image buffer at the moment when the pattern is aligned with the previous cycle. This analogy is the basis of the term ‘strobed’ temporal integration (STI) used to describe the image construction process. The details of the strobe mechanism are described in Chapter XXX.

When a sound is played twice at two points in time separated by more than 100 ms, the auditory events produce by the sounds are the same; that is, a sequence of video frames of the {γ,σ} plane would be the same. Thus, the auditory image is time-shift covariant in the time dimension for auditory events separated by about 100 ms (3.3 half lives). This is the form of time-shift covariance that is required to explain auditory perception. When a sound is repeated without a pause, the end of one presentation will interact with the start of the next presentation in the {γ,σ} plane; so this model of auditory perception is not time-shift covariant in the short term, but neither is auditory perception. Sounds do interfere with each other when presented too close in time. [[[Maybe we should try to demonstrate this experimentally. It might provide a method for measuring the half life.]]]

In summary, the auditory events associated with syllables and musical notes that form, exist and decay away in this time-averaged, scale-shift-covariant, auditory image, do so in a way that is commensurate with what we experience. The image of a stationary sound builds up over about 100 ms and decays away when the sound stops in about the same amount of time. When events occur at a rate of five per second or less, they are heard as separate events; as the rate of events rises to ten per second, the events begin to interact and time-shift covariance breaks down. Here, then, is a dynamic representation of our auditory image that produces auditory figures of communication sounds that could serve as the basis of auditory object analysis in the brain. The auditory image and the auditory events produced by communication sounds are the topic of this book.

After a little experience, this version of auditory image space, and the auditory figures that appear in it, are not nearly so strange as they might at first seem. The logarithmic scale dimension is quite similar to the place dimension of the cochlea, so this aspect of the transform requires no further explanation. The mathematical requirement that time be expanded by channel frequency, reduces to a very simple physiological dimension, namely, cycles of the resonance. This means that the auditory figures that appear in the {γ,σ} plane (Fig. 2.4.1) have a very simple interpretation. Within each channel of the sound, the hair cells are collectively recording the time and relative amplitude of the peaks of the resonance as it occurs in that channel. The vertical position of a channel in the image codes the scale of the cycles in that channel in a metric that is directly related to meters/cycle. Thus, this representation provides a detailed view of the resonances in a sound, ordered in terms of the size of the vibrating components in the source.

Finally, it should be noted that, in the presence of irregular and aperiodic sounds, these mechanisms, which are specialized for the processing of pulse-resonance sounds, degrade gracefully, strobing randomly on the larger neural peaks and producing more-or-less random distributions of activity in the auditory image. In this case, the processing reverts to a quasi-linear form that is basically driven by the short-term distribution of energy across scale.

The strobe mechanism is somewhat analogous to the windowing operation in the construction of the spectrogram. The window confines the Fourier integral to the relevant region of time. In strobed temporal integration, however, the ‘window’ position is synchronized to the pulse times and the window duration is continuously adjusted to the pulse period of the sound. There are pitch-synchronous spectrographic processors which adjust the frame size to the pitch period but the window is symmetric in time and all of the fine-structure within the window is lost in the construction of the spectrogram. The auditory image and the spectrogram are compared as models of auditory perception, and for their value as ASR preprocessors in Chapter YYY.

The description of the auditory image to this point might give the impression that all of the information that appears in the time-averaged, {γ,σ} plane passes on up the auditory pathway to the brain – something like a stream of snapshots of the instantaneous auditory image in the {γ,σ} plane. This is probably not a correct model of auditory perception with regard to data rate; there is probably a process operating on the instantaneous version of the auditory image that is designed to reduce the data rate while preserving the information, and the auditory event we experience is probably based on that reduced representation of the sound. The original data rate of the sound (around 40 Kbytes/s) has to be preserved in all channels during the construction of the auditory image to ensure that the self-segregation of features operates properly, that the features are preserved in their entirety, and that they appear in a shift-covariant form. However, once this representation is constructed, it can be summarized in representation with a much reduced data rate. For example, the 2-D envelope of the auditory figure contains most of the useful information in the auditory image, and it changes relatively slowly over periods of the sound. So both the resolution of the pattern and the rate of frames can be considerably reduced once the auditory image itself has been created. The form of the information in the auditory image and the auditory figures of pulse-resonance sounds is discussed in Chapter XXX.

Covariance and invariance in the profiles of the auditory image

The profiles of the auditory image provide an interesting tradeoff between the desire to preserve image information and the desire to reduce the data rate. Moreover, there are readily calculable. The log2c and log2s profiles of the auditory images in Fig. 2.3 are presented in the upper and lower panels of Fig. 2.5, respectively. There are four profiles in each panel, one from each panel of Fig. 2.3.

The four log2c profiles in the upper panel of Fig. 2.5 were produced by averaging over the log2s dimension of the auditory image. These log2c profiles are essentially the same; this illustrates the concept of shift invariance and the fact that the log2c profile is scale-shift invariant. It is also period-shift invariant so long as the period is longer than the resonances. Since strobing is phase locked to the pulses in the sound, the shape of the profile reflects the average decay rate of the resonances in the source, and the resonances have been expanded by channel frequency so the profile is not dominated by the decay of the narrowest resonance (typically the first formant in speech). As a result, the log2c profile reveals characteristic differences between classes of sources like ‘front’ and ‘back’ vowels. Thus, when analysing changes in the log2s profile, the lnc profile can reveal when a change the log2s-profile represents a change in source size, rather than a change of vocal tract shape.

The four log2s profiles in the lower panel of Fig. 2.5 were produced by averaging over the lnc dimension of the auditory image. The four log2s profiles form two pairs that are essentially superimposed. This illustrates the concept of shift covariance; the distribution in the profile shifts as a unit when source scale changes, so the log2s profile is scale-shift covariant. The log2s profile is also period-shift invariant, as indicated by the superposition of the profiles from vowels with different pulse periods. The individual resonances in a pulse-resonance source produce horizontal bands of activity in the auditory figure they produce, and the log2s profile provides a compact, and relatively pure, representation of this formant information.

The properties of the profiles and their potential as feature sources for speech recognition are discussed in Chapter XXX. If it is important to represent a sound by a sequence of one-dimensional vectors, as in ASR, then a scaleogram constructed of snapshots of the log2s profile, at regular time intervals, would appear to be a good candidate. It is a time-scale representation of sound that would function like the spectrogram but with the advantage that it is scale-shift covariant. The form of the scaleogram is discussed in Chapter XXX.

The voice pitch information can be included in the log2s profile by summing the activity on the period diagonal and plotting the strength of the activity in the log2s profile at the point where the diagonal intersects the ordinate, which is the scale of the pulse period. It is information about the rate at which the resonance pattern repeats, rather than information about which values of acoustic scale carry the energy of the sound. Nevertheless, it reflects acoustic scale inasmuch as the resonators that determine the pulse period increase in size with the size of the individual, albeit at a different rate.

Retrieved from "http://www.acousticscale.org/wiki/index.php/The_Space_of_Auditory_Perception"
Personal tools
Namespaces
Variants
Views
Actions
Navigation