AIM2006Modules

From CNBH Acoustic Scale Wiki

Introduction

		PCP: none
Resonance Rate (scale)	122
	89
		110	256
		Pulse rate (pitch)
Figure 3. Waveforms of the vowels in the external sound field. These plots are generated by choosing none in the PCP column (Pre-Cochlear Processing). Each subfigure shows a specific combination of pulse rate and resonance rate. See the text for details

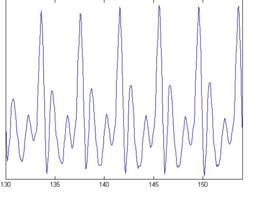
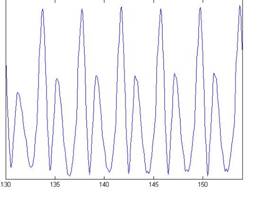
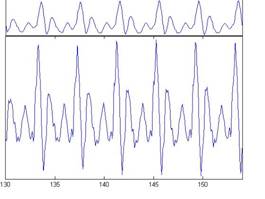
The primary concern in the examples in this document is the scaling of vowels and the normalizing of vowels scaled by STRAIGHT (Kawahara & Irino, 2004). For this purpose we use four versions of the vowel /a/ which are shown Figure 3. Each subfigure of the figure shows the waveform pertaining to a different speaker uttering the vowel sound. In the lower subfigures, the waveforms have a resonance rate of 89% of the original speaker. This corresponds to a person with a vocal tract length (VTL) of approximately 17.5 cm (6 ¾ inches) or of height of 194 cm (6'5"). In the upper subfigures are the waveforms for a resonance rate of 122% (VTL 12.7 cm or 5 inches; height 142 cm or 4'8"). The left subfigures are for a glottal pulse rate (GPR) of 110 Hz and the right subfigures for a GPR of 256 Hz. The GPR determines the pitch of the voice. The format of Figure 3 is used throughout this document to illustrate successive stages in the construction of auditory images for these four vowels, and for the size invariant Mellin magnitude images (MMI). The lower left subfigure corresponds to a large male speaker and the upper right to a small female. The lower right and upper left subfigures would correspond to somewhat unusual speakers (a castrato and a dwarf, respectively); they are included to help the reader appreciate the separate effects of a change in VTL or GPR, by identifying the salient differences between the unusual voice and the more ordinary male or female speaker.

In Figure 3, the difference in pitch is shown by the difference in pulse rate between the left and right subfigures. The effect of a resonance-rate change from 89% to 122% is most visible in the left subfigures in which the shape of the resonance following each pulse is squeezed in the upper subfigure; this is what is meant by a faster resonance rate.

PCP: pre-cochlear processing

		PCP: gm2002
Resonance Rate (scale)	122
	89
		110	256
		Pulse rate (pitch)
Figure 4. Waveforms of the vowels at the oval window of the cochlea (main panel in each subfigure) and waveforms in the external sound field (top panel in each subfigure). The format is the same as in Figure 3. These plots are generated by choosing gm2002 in the PCP column. See the text for details on the combinations of GPR and VTL.

The PCP module applies a filter to the input signal to simulate the transfer function from the sound field to the oval window of the cochlea. The purpose is to compensate for the frequency-dependent transmission characteristics of the outer ear (pinna and ear canal), the tympanic membrane, and the middle ear (ossicular bones). At absolute threshold, the transducers in the cochlea are assumed to be equally sensitive to audible sounds, so the pre-processing filters apply a transfer function similar to the shape of hearing threshold under various assumptions.

The default version of PCP is gm2002: It applies the loudness contour described by Glasberg and Moore (2002).

There are actually four different PCP filters available for different applications:

1. maf: Minimum Audible Field.
2. map: Minimum Audible Pressure.
3. elc: Equal-Loudness Contour compensation
4. gm2002: The loudness contour described by Glasberg and Moore (2002).
5. none: No pre-processing.

The threshold curves are all implemented with FIR techniques. Compensation is included to remove the time delay associated with the FIR filtering, so that the user is unaware of the shifts.

Background

Elc, map and maf are defined in Glasberg and Moore (1990). maf is appropriate for signals presented in free field; map is appropriate for systems that produce a flat frequency response at the eardrum. Options elc and gm2002 include the factors associated with the extra internal noise at low and high frequencies, in addition to the transfer function from sound field to oval window. Specifically, elc uses a correction based on equal-loudness contours at high levels (ISO 226, 1987) (Glasberg and Moore, (1990)). Gm2002 is essentially the same as elc but it is based on the more recent data of Glasberg and Moore (2002).

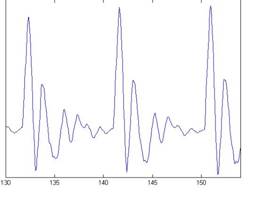
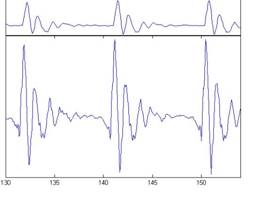
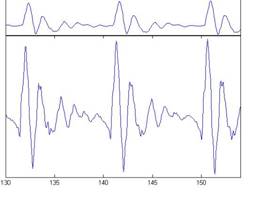
Figure 4 shows the result of applying the gm2002 transfer function to the four vowel sounds in Figure 3. The input waves are presented in the upper panel of each subfigure; the filtered waves are presented in the middle panel of each subfigure in the same format as in Figure 3. Speech sounds are, by their nature, compatible with the range of human hearing and so the effect of the transfer function is very limited; it is discernable in slight changes in the microstructure of the resonances. The input and filtered waves are aligned in time; that is, compensation is included to remove the time delay associated with the FIR filtering.

BMM: basilar membrane motion

AIM simulates the spectral analysis performed in the cochlea with an auditory filterbank, which is intended to simulate the motion of the basilar membrane (in conjunction with the outer hair cells) as a function of frequency and time. There is essentially no temporal averaging, in contrast to spectrographic representations where segments of sound 10 to 40 ms in duration are summarized in a spectral vector of magnitude values. Aim2006 simulates the basilar membrane motion (BMM) produced by the input sound with one of four filterbanks.

The default filterbank is dcgc: the dynamic, compressive gammachirp filterbank (Irino & Patterson, 2006). The dcgc filters have level-dependent asymmetry, and fast acting compression is applied between the first and second stages of the dcgc filter. The filter architecture and its operation are described below.

There are actually four auditory filterbanks available for different applications:

1. dcgc: The dynamic compressive gammachirp filterbank,
2. gc: The gammachirp filterbank: A time-domain version of the filter in Patterson et al. (2003),
3. wl: The wavelet filterbank: A time-domain version of the wavelet defined in Reimann (2006), and
4. gt: The gammatone filterbank: the traditional auditory filterbank of Patterson et al. (1995).
5. none: No auditory filterbank.

Background

Previous versions of AIM simulated the spectral analysis performed by the auditory system with a linear gammatone (GT) auditory filterbank (Cooke, 1993; Patterson & Moore, 1986; Patterson et al., 1992). There are three well known problems with using the GT filterbank as a simulation of cochlear filtering:

1. The filters were essentially symmetric on a linear frequency scale which is similar to the auditory filter at low stimulus levels. However, in the auditory system the filters become progressively broader and more asymmetric as level increases.
2. There is no compression in a GT filterbank. There is no compression in auditory filtering at high stimulus levels (above 85 dB SPL), but as level decreases the system applies more and more gain in the region of the tip of the filter which means that the input/output function of the basilar membrane (in combination with the outer hair cells) is strongly compressive. Previously in AIM, compression was applied as part of the transduction process that follows the GT filterbank.
3. Auditory compression is fast-acting; the compression varies dynamically within the glottal cycle. It compresses glottal pulses relative to the formant resonances that follow the glottal pulse. As a result, it restricts the dynamic range while maintaining good frequency resolution for the analysis of vocal-tract resonances (Irino & Patterson, 2006). It is argued that this dynamic adjustment of filter properties improves the robustness of speech recognition by raising the relatively low level of the formants with respect to the relatively high level of the glottal pulses. An extended example is presented in Irino and Patterson (2006, Figures 7, 8 and 9).

The compressive gammachirp filter

The compressive gammachirp (GC) filter is a generalized form of the gammatone filter, which was derived with operator techniques (Irino & Patterson, 1997). It was designed to simulate the properties of the auditory filter measured experimentally in the past 15 years. The development of both the gammatone and gammachirp filters is described in Patterson et al. (2003, Appendix A).

Figure 5. Illustration of (a) the construction of an asymmetric, passive gammachirp filter (GC) from a symmetric gammatone filter (GT) and a low-pass asymmetric function (LP-AF), and (b) the construction of a set of compressive gammachirp filters (GC) from one passive GC filter and a high-pass asymmetric function (HP-AF) whose center frequency shifts up as stimulus level increases. The vertical dotted lines show the peak frequencies of (a) the passive GC and GT filters (left and right, respectively) and (b) the passive GC filter. Figure from Patterson et al. (2003).

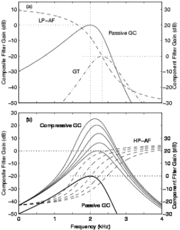
The compressive gammachirp (cGC) filter is composed of a passive gammachirp (pGC) filter and a High-Pass Asymmetric Function (HP-AF) arranged in cascade as shown in Figure 5 (Figure 1 in Patterson et al., 2003). The pGC filter simulates the action of the passive basilar membrane and the output of the pGC filter is used to adjust the level dependency of the active part of the filter, which is the HP-AF. The HP-AF is intended to represent the interaction of the cochlear partition with the tectorial membrane as suggested by Allen (1997) and Allen and Sen (1998). The effect is to sharpen the low-frequency side of the combined filter, which produces a tip in the cGC filter shape at low to medium stimulus levels (Figure.1a). Note, however, that there is no high-frequency side to this tip filter; it only produces high-pass filtering and level-dependent gain in the region of the peak frequency. The fact that there is no high-frequency side to the tip filter keeps the number of parameters to a minimum and avoids the instabilities encountered with the parallel filter systems where the high-frequency sides of the tip and tail filters interact.

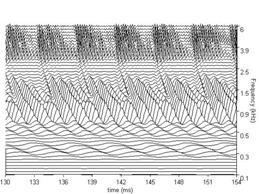
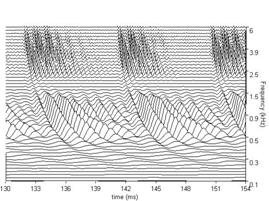
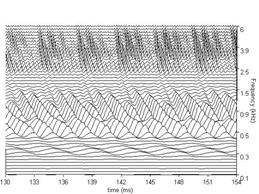
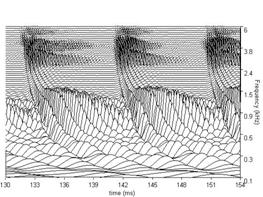
In Patterson et al. (2003), this cascade cGC filter was fitted to the combined notched-noise masking data of Glasberg and Moore (2000) and Baker et al. (1998). It was found that most of the effect of center frequency could be explained by the function that describes the c hange in filter bandwidth with center frequency. Patterson et al. (2003) expressed the parameters describing the filter as a function of ERBN-rate (Glasberg & Moore, 1990), where ERBN stands for the average value of the equivalent rectangular bandwidth of the auditory filter, as determined for young normally hearing listeners at mo derate sound levels (Moore, 2003). Once the parameters were written in this way, the shape of the cGC filter could be specified for the entire range of center frequencies (0.25-6.0 kHz) and levels (30-80 dB SPL) using just six fixed coefficients. The families of cGC filters derived in this way are illustrated in Figure. 6 for probe frequencies from 0.25 to 6.0 kHz.

Figure 6. Families of compressive gammachirp filters (a) for probe frequencies from 0.25 to 6.0 kHz. The component filters (b) are presented for four probe frequencies, 0.25, 1.0, 3.0 and 6.0 kHz; the remainder are omitted for clarity. The six curves within each set of cGC filters (a) and HP-AFs (b) show how the functions change as probe level increases from 30 to 80 dB in 10 dB steps. Figure from Patterson et al. (2003).

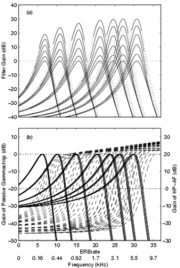
The cascade cGC filter has several advantages: (a) The compression it applies is largely limited to frequencies close to the center frequency of the filter, as happens in the cochlea (Recio, Rich, Narayan, & Ruggero, 1998); (b) The form of the chirp in the impulse response is largely independent of level, as in the cochlea (Carney, McDuffy, & Shekhter, 1999); (c) The impulse response can be used with an adaptive control circuit to produce a dynamic, compressive gammachirp filter (Irino & Patterson, 2005, 2006) to enable auditory modeling in which fast-acting compression is applied as part of the filtering process.

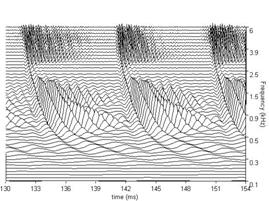
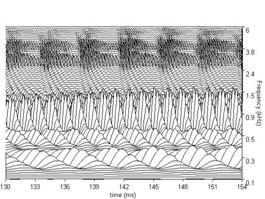
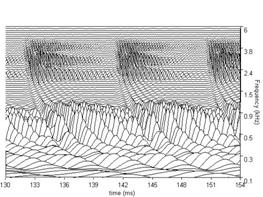
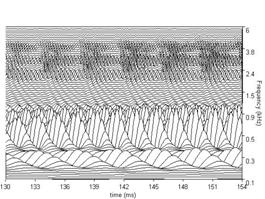
The BMM produced by the dcgc filterbank in response to each of the four /a/ vowels in Figure 3, is presented in Figure 7. The four subfigures show the BMM for the vowel in the corresponding subfigure of Figure 3. The concentrations of activity in channels above 0.5 kHz show the resonances of the vocal tract. They are the 'formants' of the vowel. The sinusoidal activity in the lowest channels represents the fundamental or second harmonic which is typically resolved for vowels; this activity is attenuated in the auditory system by the outer and middle ear transfer function which is simulated by the gm2002 option of the PCP modules. The duration of the segment of each panel of BMM is 24 ms. There are 100 channels in the filterbank in this example and they cover the frequency range of 100 to 6000 Hz. All of these parameters can be modified either directly in the control window or via the parameter file.

		BMM: dcgc
Resonance Rate (scale)	122
	89
		110	256
		Pulse rate (pitch)
Figure 7a. Basilar Membrane Motion(BMM) for the four example vowels produced by the dynamic compressive gammachirp filterbank. The subfigures are presented in the same format as in Figure 3. These plots are generated by choosing gm2002 in the PCP column and dcgc in the BMM column. See the text for details on the combinations of GPR and VTL.

Figure 7a shows the BMM for the four example vowels using the dcGC filterbank option; for comparison, Figure 7b shows the BMM for the same vowels using the gammatone filterbank. Note that there is a difference in the form and the relative strength of the formants; the dcGC filters are compressive and so the formant information is spread across more channels. The formants in the BMMs of the gammatone filters appear sharper at this stage. However, this apparent sharpness is spurious in the sense that this pattern does not actually occur on the basilar membrane. In traditional auditory models, the filterbank is linear and compression is applied at the output of the filterbank as if it were part of the neural transduction stage (described in 3.3 below). The dcGC filterbank may be unique in having fast-acting compression within the auditory filter, in a computational model. The differences in resonance rate are discernable in the low-pitch examples in the left-hand subfigures. The latency of the peaks that make up the ridges corresponding to the glottal pulses increase as frequency decreases. This is referred to as the propagation delay of the cochlea. Note, however, that the propagation delay is much less in the dcGC filterbank, so the channels are better aligned in time.

		BMM: gt
Resonance Rate (scale)	122
	89
		110	256
		Pulse rate (pitch)
Figure 7b. Basilar Membrane Motion (BMM) for the four example vowels produced by the traditional gammatone filterbank. The subfigures are presented in the same format as in Figure 3. These plots are generated by choosing gm2002 in the PCP column and gt in the BMM column. See the text for details on the combinations of GPR and VTL.

In Figures 7a and 7b, each plot has 100 frequency channels. The figures are generated using the MATLAB 'waterfall' plotting function, and then exported as jpg files. The default plot type in aim2006 for the BMM stage is actually 'mesh', because it renders much faster, and for most everyday uses, its resolution is sufficient. It is also sometimes useful to reduce the number of frequency channels to 50 to achieve faster graphics rendering. When high-quality figures are required for printed presentation or videos, the plot type can be changed to 'waterfall’ in the file parameters.m for the graphics module in question (e.g. /aim-mat/modules/graphics/dcgc/ for the dcgc filterbank).

NAP: Neural Activity Pattern

		NAP: hl(dcgc)
Resonance Rate (scale)	122
	89
		110	256
		Pulse rate (pitch)
Figure 8a. Neural Activity Patterns for the four example vowels produced by the dynamic compressive gammachirp filterbank and half-wave rectification (main panel in each subfigure). The tonotopic profile in the right-hand panel of each subfigure shows the average of the neural activity over time; this representation is often referred to as an excitation pattern. The subfigures are presented in the same format as in Figure 3. These plots are generated by choosing gm2002 in the PCP column and dcgc in the BMM column; the NAP column defaults to hl.

The BMM is converted into a simulation of the neural activity pattern (NAP) observed in the auditory nerve using one of the ‘neural transduction’ modules in the NAP column (Patterson et al., 1995).

The default NAP depends upon the choice of filterbank. For the default filterbank, dcgc, it is hl, and for the traditional filterbank, gt, it is hcl.

There are four NAP modules available:

1. hl: Half-wave rectification and lowpass filtering (for the dcgc filterbank),
2. hcl: Half-wave rectification, logarithmic compression and lowpass filtering (for the gt filterbank),
3. 2dat: Two-dimensional adaptive threshold (Patterson & Holdsworth, 1996),
4. none: No neural transduction.

Background

The default module for gt filterbank is hcl which consists of three sequential operations: half-wave rectification, compression and low-pass filtering.

The half-wave rectification makes the response to the BMM uni-polar like the response of the hair cell, while keeping it phase-locked to the peaks in the wave. Experiments on pitch perception indicate that the fine structure is required to predict the pitch shift of the residue (Yost, Patterson, & Sheft, 1998). Other rectification algorithms like squaring, full-wave rectification and the Hilbert transform only preserve the envelope.

The compression is intended to simulate the cochlear compression that is absent in the gammatone filters; the compression reduces the slope of the input/output function. Compression is essential to cope with the large dynamic range of natural sounds. It does, however, reduce the contrast of local features such as formants. This is evident in the output of dcgc filterbank which has internal compression, and also in the output of the gt/hcl combination where the compression follows the filterbank. The default form of compression is square root since that appears to be close to what the auditory system applies. Aim2006 also offers logarithmic compression to be compatible with earlier versions of AIM, and to support speech recognition systems that benefit from the level-independence that this imparts to the NAP.

The low-pass filtering simulates the progressive loss of phase-locking as frequency increases above 1200 Hz. The default version of hcl applies a four stage low-pass filter which completely removes phase locking by about 5 kHz.

Hcl is widely used because it is simple, but it lacks adaptation and as such is not realistic. A more sophisticated solution is provided by the 2dat module (2-dimensional adaptive-thresholding) (Patterson & Holdsworth, 1996). It applies global compression like hcl but then it restores local contrast about the larger features with adaptation, both in time and in frequency. When using compressive auditory filters like the dcGC there is no need for compression in the NAP stage, and therefore the default NAP for the dcgc filter option is hl.

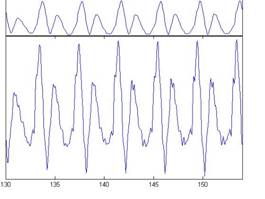
Figure 8a shows the NAPs for the four example vowels with the dcgc/hl combination of options. The tonotopic profile on the right of the NAP shows the sum of the activity in the window across time; this representation is often referred to as an excitation pattern (Glasberg & Moore, 1990). The formants can be seen as local maxima in this profile. A comparison of the NAPs in Figure 8a with the BMMs in Figure 7a shows that the representation of the higher formants is actually sharper than in the BMM. Figure 8b shows the NAPs for the four example vowels with the gt/hcl combination of options. A comparison of the NAPs in Figure 8b with the BMMs in Figure 7b shows that compression reduces the contrast of the representation around the formants.

SF: Strobe Finding

This module finds strobe points (SP) in the individual channels of the NAP. These points correspond to maxima in the NAP pattern like those produced when glottal pulses excite the filterbank. The strobe pulses enable the segregation of the pulse and resonance information and they control pulse-rate normalisation. Auditory image construction is robust, in the sense that strobing does not have to occur exactly once per cycle to be effective, however, the most accurate representation of the resonance structure is produced with accurate, once-per-cycle strobing.

The default version of SP is sf2003

There are two different strobe modules available:

1. sf1992: the original adaptive-thresholding version of strobing (peak_threshold)
2. sf2003: this version has a more sophisticated version of adaptive thresholding.

Figure 9a. Schematic illustration of strobe finding in one channel of the NAP for the vowel /a/ using the sf2003 module. In the example the centre frequency is 1.2 kHz. The strobes are marked by black dots and they occur where the NAP rises above the adaptive threshold which is indicated with a black line above the signal waveform.

Background

Perceptual research on pitch and timbre indicates that at least some of the fine-grain time-interval information in the NAP is preserved in the auditory image (e.g. Krumbholz, Patterson, Nobbe, & Fastl, 2003; Patterson, 1994a, 1994b; Yost et al., 1998). This means that auditory temporal integration cannot, in general, be simulated by a running temporal average process, since averaging over time destroys the temporal fine structure within the averaging window (Patterson et al., 1995). Patterson et al. (1992) argued that it is the fine-structure of periodic sounds that is preserved rather than the fine-structure of noises, and they showed that this information could be preserved by a) finding peaks in the neural activity as it flows from the cochlea, b) measuring time intervals from these strobe points to smaller peaks, and c) forming a histogram of the time-intervals, one for each channel of the filterbank. This two-stage temporal integration process is referred to as ‘strobed’ temporal integration (STI). It stabilizes and aligns the repeating neural patterns of periodic sounds like vowels and musical notes (Patterson, 1994a, 1994b; Patterson et al., 1995; Patterson et al., 1992). The complete array of interval histograms is AIM's simulation of our auditory image of the sound. The auditory image preserves all of the fine-structure of a periodic NAP if the mechanism strobes once per cycle on the largest peak (Patterson, 1994b; Patterson et al., 1992), and provided the image decays exponentially with a half life of about 30 ms, then it builds up and dies away with the sound as it should.

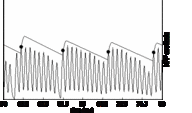
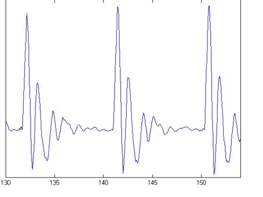
Aim2006 currently includes two strobe finding algorithms, sf1992 and sf2003. The older module, sf1992, operates on simple adaptive-filtering logic; it is included for demonstration purposes and to provide backward compatibility with previous versions of AIM. The newer strobe-finding module, sf2003, uses a more sophisticated adaptive thresholding mechanism to isolate strobe points. The process used by sf2003 is illustrated in Figure 9a, which shows one channel of the NAP, the adaptive threshold and strobe points; the centre frequency of the channel is 1.2 kHz. A strobe is issued when the NAP rises above the adaptive strobe-threshold; the strobe time is that associated with the peak of the NAP pulse. Following a strobe, threshold initially rises along a parabolic path and then returns to the linear decay to avoid spurious strobes. The duration of the parabola is given by the centre frequency of the channel; its height is proportional to the height of the strobe point. After the parabolic section of the adaptive threshold, its level decreases linearly to zero in 30 ms. The adaptive threshold and strobe points appear automatically when the single channel option is used with the SP display. Note that this simple mechanism locates one strobe per cycle of the vowel in this channel. Figures 9b and 9c show the strobe points located in all of the channels of each NAP in Figures 8a and 8b, for the gammachirp and gammatone filterbanks, respectively.

		SP: sf2003(dcgc-hl)
Resonance Rate (scale)	122
	89
		110	256
		Pulse rate (pitch)
Figure 9b. Strobe points (red dots) for the four example vowels superimposed on the the dcgc/hl NAP of the vowel in each case. The right-hand panel in each subfigure shows the excitation pattern. The subfigures are presented in the same format as in Figure 3. These plots are generated by choosing gm2002 in the PCP column, dcgt in the BMM column, hl in the NAP column and sf2003 in the SP column.

		SP: sf2003(gt-hcl)
Resonance Rate (scale)	122
	89
		110	256
		Pulse rate (pitch)
Figure 9c. Strobe points (red dots) for the four example vowels superimposed on the gt/hcl NAP of the vowel in each case. The right-hand panel in each subfigure shows the excitation pattern. The subfigures are presented in the same format as in Figure 3. These plots are generated by choosing gm2002 in the PCP column, gt in the BMM column, hcl in the NAP column and sf2003 in the SP column.

SAI: Stabilised Auditory Image

The SAI module uses the strobe points to convert the NAP into a auditory image, in which the pulse-resonance pattern of a periodic sound is stabilised. The process is referred to as Strobed Temporal Integration (STI), and it converts the time dimension of the NAP into the time-interval dimension of the stabilised auditory image (SAI). The vertical ridge in the auditory image associated with the repetition rate of the source can be used to identify the start point for any resonance in that channel, and this makes it possible to completely segregate the glottal pulse rate from the resonance structure of the vocal tract. To repeat, the abscissa of the SAI is now no longer time but time interval, and the structure in each channel is what physiologists would refer to as a post-glottal pulse, time-interval histogram.

The default SAI is ti2003. The are two SAI modules available:

1. ti2003: this version adapts temporal integration to the strobe rate; that is, the higher the rate, the smaller the proportion of each NAP pulse that is added in to the auditory image.

1. ti1992: Temporal integration of the NAP pulses into an array of time-interval histograms referred to as the auditory image (Patterson, 1994b)(Patterson et al., 1992).

Background

Once the strobe points have been located, the NAP can be converted into an auditory image using STI, which is a discrete form of temporal integration. Aim2006 offers two SAI options for performing the conversion: ti1992 and ti2003. Strobed temporal integration converts the time dimension of the neural activity pattern into the time-interval dimension of the stabilized auditory image (SAI) image, and it preserves the time-interval patterns of repeating sounds (Patterson et al., 1995).

The ti1992 module (Patterson, 1994b; 1992) works as follows: When a strobe is identified in a given channel, the previous 35 ms of activity is transferred to the corresponding channel of the auditory image, and added, point for point, to the contents of that channel of the image. The peak of the NAP pulse that initiates temporal integration is mapped to the 0-ms time-interval in the auditory image. Before addition, however, the NAP level is progressively attenuated by 2.5% per ms, and so there is nothing to add in beyond 40 ms. This 'NAP decay' was implemented to ensure that the main pitch ridge in the auditory image would disappear as the period approached that associated with the lower limit of musical pitch which is about 32 Hz (Pressnitzer, Patterson, & Krumbholz, 2001). The fact that ti1992 integrates information from the NAP to the auditory image in 35-ms chunks leads to short-term instability in the amplitude of the auditory image. This is not a problem when the view is from above as in the main window of the auditory image display. It is, however, a problem when the tonotopic profile of the auditory image is used as a pre-processor for automatic speech recognition because some of these devices are particularly sensitive to level variability.

The default SAI module is ti2003 which is causal and eliminates the need for the NAP buffer. It also reduces the level perturbations in the tonotopic profile, and it reduces the relative size of the higher-order time intervals as required by more recent models of pitch and timbre (Kaernbach & Demany, 1998; Krumbholz et al., 2003). It operates as follows: When a strobe occurs it initiates a temporal integration process during which NAP values are scaled and added into the corresponding channel of the SAI as they are generated; the time interval between the strobe and a given NAP value determines the position where the NAP value is entered in the SAI. In the absence of any succeeding strobes, the process continues for 35ms and then terminates. If more strobes appear within 35 ms, as they usually do in music and speech, then each strobe initiates a temporal integration process, but the weights on the processes are constantly adjusted so that the level of the auditory image is normalised to that of the NAP: Specifically, when a new strobe appears, the weights of the older processes are reduced so that older processes contribute relatively less to the SAI. The weight of process n is 1/n, where n is the number of the strobe in the set (the most recent strobe being number 1). The strobe weights are normalised so that the total of the weights is 1 at all times. This ties the overall level of SAI more closely to that of the NAP and ensures that the tonotopic profile of the SAI is like that of the NAP at all times.

Nomenclature: Normally, the sf2003 is used with ti2003, and sf1992 is used with ti1992. In such cases, for convenience, the combinations are referred to as sti03 and sti92, respectively.

Figure 10a shows the SAIs for the four example vowels using the dcgc/hl/sti03 model. Note the strong vertical ridge at the time interval associated with the pitch of the vowel. The resonance information now appears aligned on the vertical ridge. There are also secondary cycles at lower levels. The tonotopic profiles in the right-hand panels of the subfigures present a clear representation of the formant structure of each vowel, and the tonotopic profiles in the upper row of the figure for the scale value of 122 are shifted up relative to those in the lower row where the scale value is 89.

The time-interval profile in the panel below each auditory image shows the average across the channels of the auditory image. It shows that in periodic sounds, the ridges beside the vertical ridge associated with the pitch of the sound have a slant (the time interval between the vertical ridge and the slanting adjacent ridges is 1/f ms, so it degrease as f increases), and this means that the peaks in the time-interval profile associated with the adjacent ridges are small relative to that of the main vertical ridge. This feature improves pitch detection when it is based on the time-interval profile.

Figure 10b shows the SAIs for the four example vowels using the gt/hcl/sti03 model. They also exhibit strong vertical ridges at the time interval associated with the pitch of the vowel. The resonance structure is anchored to the vertical ridge but the details of the fine structure of the lower formants are less clear due to the log compression. The tonotopic profiles in the right-hand panels of the subfigures show that the lower formants are less clear but the upper formants are more clear.

		SAI: ti2003(dcgc-hl-sf2003)
Resonance Rate (scale)	122
	89
		110	256
		Pulse rate (pitch)
Figure 10a. Stabilized Auditory Images (SAI) for the four example vowels. The lower panel in each subfigure shows the time-interval profile, and the right-hand panels of the subfigure show the tonotopic profiles. The subfigures are presented in the same format as in Figure 3. These plots are generated by choosing gm2002 in the PCP column, dcgc in the BMM column, hl in the NAP column, sf2003 in the SP column and ti2003 in the SAI column.

Dynamic sounds

For periodic and quasi-periodic sounds, STI rapidly adapts to the period of the sound and strobes roughly once per period. In this way, it matches the temporal integration period to the period of the sound and, much like a stroboscope, it produces a static auditory image of the repeating temporal pattern in the NAP as long as the sound is stationary. If a sound changes abruptly from one form to another, the auditory image of the initial sound collapses and is replaced by the image of the new sound. In speech, however, the rate of glottal cycles is typically large relative to the rate of change in the resonance structure, even in diphthongs, so the auditory image is like a high-quality animated cartoon in which the vowel figure changes smoothly from one form to the next. The dynamics of these processes can be observed using aim2006, and the frame rate can be adjusted to suit the dynamics of the sound and the analysis. It is also possible to generate a QuickTime movie with synchronized sound for reviewing with standard media players.

Time-interval scale (linear or logarithmic): aim2006 offers the option of plotting the SAI on either a linear time-interval scale as in previous versions of AIM, or on a logarithmic time-interval scale. The latter was implemented for compatibility with the musical scale. Vowels and musical notes produce vertical structures in the SAI around their pitch period, and the peak in the time-interval profile specifies the pitch. If the SAI is plotted on a logarithmic scale then the pitch peak in the time-interval profile moves equal distances along the pitch axis for equal musical intervals. The time-intervalscale can be set to linear in the parameter file for the ti-module; change the value of the variable ti2003.

		SAI: ti2003(gt-hcl-sf2003)
Resonance Rate (scale)	122
	89
		110	256
		Pulse rate (pitch)
Figure 10b. Stabilized Auditory Images (SAI) for the four example vowels. The lower panel in each subfigure shows the time-interval profile, and the right-hand panels of the subfigure show the tonotopic profiles. The subfigures are presented in the same format as in Figure 3. These plots are generated by choosing gm2002 in the PCP column, gt in the BMM column, hcl in the NAP column, sf2003 in the SP column and ti2003 in the SAI column.

Autocorrelation: The time-interval calculations in AIM often provoke comparison with autocorrelation and the autocorrelogram (Meddis & Hewitt, 1991), and indeed, models of pitch perception based on AIM make similar predictions to those based on autocorrelation (Patterson, Yost, Handel, & Datta, 2000). It should be noted, however, that the autocorrelogram is symmetric locally about all vertical pitch ridges, and this limits its utility with regard to aspects of perception other than pitch. For example, it cannot explain the changes in perception that occur when sounds are reversed in time (Akeroyd & Patterson, 1997; Patterson & Irino, 1998) whereas the SAI can.

MMI: Mellin Magnitude Image

Aim2006 has a Development module for research on the auditory image and modelling of more central auditory processes based on auditory images. At the CNBH, there are currently three development projects which appear in this column of the aim2006 GUI; one is concerned with pitch perception and the other two are concerned with the invariance problem in speech and music, that is, the fact that human perception of speech and music sources is largely immune to changes in pulse rate and resonance rate (Ives, Smith, & Patterson, 2005; Smith & Patterson, 2005; Smith, Patterson, Turner, Kawahara, & Irino, 2005).

The default option is the Mellin transform, mt, which produces a Mellin Magnitude Image (MMI). It is a size invariant representation of the resonance structure of a source. In the MMI, vowels scaled in GPR and VTL produce the same pattern in the same position within the image. The processing is a two-dimensional form of Mellin transform (mt) in which both the time-interval dimension and the tonotopic frequency dimension are transformed to produce the scale-invariant representation.

The three present Development modules convert the SAI into three new representations:

1. mt: the Mellin Transform produces a size invariant representation of the resonance structure of the source.
2. sst: Size Shape Transform produces a size covariant representation of the resonance structure of the source.
3. dpp: the Dual Pitch Profile is a coordinated log-frequency representation of the time-interval profile and the tonotopic profile of the auditory image.

Background

Human perception of speech and music sources is largely immune to changes in the pulse rate and the resonance rate in the sounds (Ives et al., 2005; Smith & Patterson, 2005; Smith et al., 2005); that is, the parameters associated with source size.

The Mellin transform module, mt, converts the SAI into a Mellin Magnitude Image (MMI). It is a size-invariant representation of the resonance structure of a source. In the MMI, vowels scaled in GPR and VTL produce the same pattern in the same position within the image. The processing is a two-dimensional form of Mellin transform (mt) in which both the time-interval dimension and the tonotopic frequency dimension are transformed to produce the size-invariant representation. Versions of AIM with gammatone or gammachirp filterbanks, strobed temporal integration and the Mellin transform all produce versions of what Irino and Patterson (2002) refer to as Stabilised Wavelet Mellin Transforms. They all produce size-invariant representations of the resonance structure of a sound.

Figure 11a shows the MMIs for the four example vowels using the dcgc/hl/sti03/mt model. The envelopes of the patterns for the four vowels are much more similar than in previous representations. That is, the portions of the plane that are occupied are highly correlated and the structure of the pattern within regions is similar. Thus, the variability due to GPR and VTL has essentially been removed from the representation. There are differences in the fine structure of the patterns which result from the degree to which the resonance fits between adjacent glottal pulses in each of the vowels.

Figure 11b shows the MMIs for the four example vowels using the gt/hcl/sti03/mt model. Again, there is good correlation between the areas of the planes in the subfigures. However, the time-interval fine structure is not as well-defined and regular as in Figure 11a in which the dcgc/hl/sti03/mt model was used. Qualitatively, the plots in Figure 11b seem to be more invariant to scale changes (VTL) than to pitch changes (GPR); this is in contrast to Figure 11a.

The Size Shape Transform is an alternative transform of the auditory image that is size covariant, rather than size invariant. The distinction derives from the operator mathematics used to derive the MMI. In the scale covariant image (SSI), vowels scaled in GPR and VTL produce the same pattern in the SSI, but the position of the pattern moves vertically in the tonotopic dimension with changes in scale, and the pattern shifts linearly with scale. This representation has several advantages that are currently being explored. The pattern of resonances has an intuitive form. It does not change with size and the size information appears in a compact form independent of the resonance pattern.

		MMI: mt(dcgc-hl-sf2003-ti2003)
Resonance Rate (scale)	122
	89
		110	256
		Pulse rate (pitch)
Figure 11a. Mellin Magnitude Images for the four example vowels. The subfigures are presented in the same format as in Figure 3. These plots are generated by choosing gm2002 in the PCP column, dcgt in the BMM column, hl in the NAP column, sf2003 in the SP column, ti2003 in the SAI column, and finally mt in the Development column.

The Dual Pitch Profile is intended for research into the relationship between pitch information in the time-interval profile and the tonotopic profile of the auditory image. It provides a frequency coordinated combination of the time-interval profile and the tonotopic profile to reveal which form of pitch information dominates the perception in a given sound.

The user can also define new Development modules and add them to the menu. Indeed, they can add modules to any of the columns. There is web-based documentation (http://www.pdn.cam.ac.uk/cnbh/aim2006) with examples to explain the process of adding a new module.

		MMI: mt(gt-hcl-sf2003-ti2003)
Resonance Rate (scale)	122
	89
		110	256
		Pulse rate (pitch)
Figure 11b. Mellin Magnitude Images for the four example vowels. The subfigures are presented in the same format as in Figure 3. These plots are generated by choosing gm2002 in the PCP column, gt in the BMM column, hcl in the NAP column, sf2003 in the SP column, ti2003 in the SAI column, and finally mt in the Development column.

MOVIE: movies with synchronized sound

The auditory image is dynamic and aim2006 includes a facility for generating QuickTime movies of the SAI of any subsequent stabilized image with synchronised sound. Aim2006 calculates snapshots of the image at regular intervals in time and stores the images in frames which are then assembled into a QuickTime movie with synchronous sound to illustrate the dynamic properties of sounds as they appear in the auditory image. A movie of the SAI, can be generated by ticking the calculate box and clicking the MOVIE button. The movie is created from the bitmaps produced by aim2006 and so the movie is exactly what appears on the screen. QuickTime movies are portable and the QuickTime player is available free on the internet.