The Communication Code

From CNBH Acoustic Scale Wiki

This chapter presents a simple, formant-pattern model of speech communication that illustrates the role of speaker size and vocal-tract length in the production and perception of communication sounds.

Roy Patterson , Jessica Monaghan, Tom Walters

A simple model of vowel production

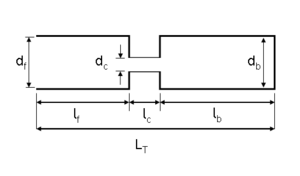
Arai (2006) has described a simple ‘three-tube’ model of vowel production that is sufficient to illustrate how the voiced sounds in speech (i.e., vowels and sonorant consonants) are produced. A schematic of the model is presented in Figure 1; it ignores much of the anatomy of the vocal tract, such as the distinction between the oral and pharyngeal cavities, and simply assumes that the tongue is used to produce a constriction in the vocal tract, which divides it into three tubes. One of the tubes, t_f, is in front of the constriction, extending forward from the constriction to the lips; one of the tubes, t_b, is behind the constriction extending from it to the larynx; and the third tube, t_c, connects the other two tubes and forms the constriction. What matters in the model are the diameters and lengths of the tubes (d_f, d_c, d_b and l_f, l_c, l_b) and the vocal tract length, L_T. It is assumed that the information communicated from speaker to listener can be summarized by the resonant frequencies, or formant frequencies, produced by the tubes when excited by a stream of glottal pulses.

Figure 1: The cavities and variables of the ‘three-tube’ model of production described by Arai (2006).

In this chapter, the focus is on the size of the components involved in the production of speech – primarily, the size of the resonators and the length of the vocal tract. The size relationships are more easily understood if the formants are described in terms of the wavelengths of the sounds they produce, rather than the corresponding frequency values; the wavelength of a resonance, λ, is the reciprocal of its frequency, f, times the speed of sound, c; that is, λ = c/f.

In general, the wavelength, λ_i, of a vocal resonator, i, is some function, R_i, times the length of the resonator, l_i, and the resonator length is some proportion, w_i, of the length of the vocal tract, L_T. So, in general,

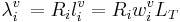(1)

The front cavity produces the second formant of the vowel; in the three-tube model, the cavity is assumed to vibrate like a tube closed at one end (the constriction), in which case, R₂ is 4, and so the wavelength, λ₂, is

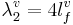(2)

The back cavity produces the third formant; the cavity is assumed to vibrate like a tube closed at both ends, in which case, R₃ is 2, so the wavelength, λ₃, is

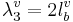(3)

The constriction acts together with the back cavity to form a Helmholtz resonator with the back cavity forming the bottle and the constriction forming the neck. The plug of air in the neck of the bottle vibrates and drives the volume of air in the body of the bottle, so the resonance function, which specifies the wavelength of the first formant, λ₁, is somewhat more complex than those for the second and third formants. It is

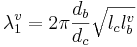(4)

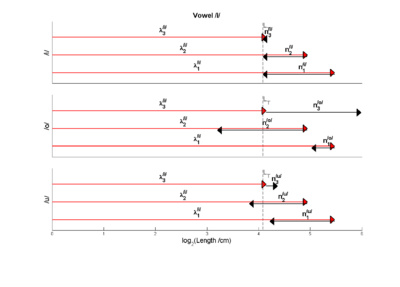
Figure 2 provides an overview of vowel communication as implied by the three-tube model, although not explicitly stated by Arai(2006). The figure has three parts, which characterize (a) the role of the resonators in producing the sound (upper panel), the set of wavelengths that summarize what is transmitted from the speaker to the listener in this model (middle panel), and the decoding of the sound in the perceptual system of the listener. The abscissa for all three panels is length in centimeters, on a logarithmic axis; so 0 is 1 cm.

Figure 2: An overview of vowel communication implied by the three-tube model. Top panel: the role of the resonators in producing the sound. Middle panel: the set of wavelengths that represent what is transmitted from the speaker to the listener. Bottom panel: the decoding of the vowel in the perceptual system of the listener. The abscissa for all three panels is length in logarithmic units.

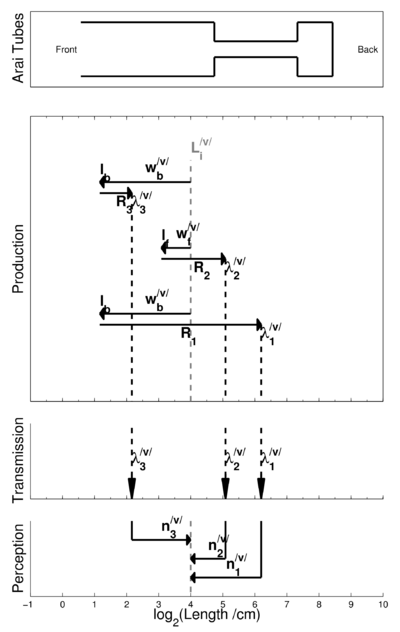
The upper panel shows how the formant wavelengths can be calculated from the speaker’s vocal tract length and the cavity-length weights for a specific vowel, which in this case is /o/, as in ‘toe.’ The speaker has a vocal tract length of 16.5 cm – a value which is commonly cited as the average for adult males. In general, for the first three formants,

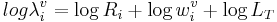(5)

In this example, one can think of the calculation as starting at the dashed grey vertical line, which shows the log of the speaker’s vocal tract length, i.e., log L_T. Then, for each resonator, the log of the length of the tube is calculated by adding the log of the weight that relates tube length to vocal tract length. Note, however, the weights are all less than one and so the log of the weight is invariably negative, and the effect is to subtract the log of the weight from log L_T. In the vowel /o/, the front cavity is large, so weight, w_f, is close to one and the logarithm of the w_f is a small negative number; in the figure the subtraction is symbolized by a leftwards pointing arrow, which ends at log l_f, the log of the length of the front tube. In /o/, the back cavity is small, so the weight, w_b, is closer to zero than one, and the logarithm of w_b is a larger negative number. The calculation of back tube length is the same for the third formant and the first formant. The leftwards pointing arrows, which end at log l_b are longer than for the front tube, and the log of the back tube length, log l_b is correspondingly smaller. Once the tube lengths have been calculated, they are converted into wavelengths by adding the log of the appropriate resonance function, log R_i; the wavelength is always longer than the tube length, so these arrows all proceed to the right ending in log λ_i values that are larger than the log of the corresponding tube length, log l_i.

The communication code

In the formant-pattern model, it is this set of three formant frequencies (λ₁, λ₂, λ₃) that communicates vowel-type from speaker to listener, as indicated by the three arrows the cross the transmission panel in the middle of the figure to the perception panel in the lower part of the figure. It is important to remember that these wavelengths provide a combination of two forms of information – information about vowel type and information about speaker size. The form of the information is rather simple, as illustrated by imagining what happens to the log-wavelength values, log λ_i, when the same vowel is produced by a woman or a child with a shorter vocal tract. The dashed grey line, that is the starting point for the wavelength calculations would move to the left, as the size of the speaker, and thus their vocal tract length, decreased. In the three-tube model, the tube-length weights, w_i, and the resonance functions, R_i, do not vary with speaker size – everything is proportional – and so the arrows that represent the calculations are fixed in length. As a result, as speaker size decreases and the vertical dashed line shifts to the left, the entire structure in the upper panel shifts to the left with it. The formant pattern remains the same. In mathematical terms, the advantage of the formant pattern as a communication code is that the representation is ‘covariant.’ That is, the representation contains VTL information as well as vowel-type information, but the two are neatly segregated in the representation, and the segregation greatly facilitates the decoding process.

Thus, with regard to perception and recognition, it is very important to know the extent to which simple models of vowel production are valid. If the communication code is the formant pattern, and this pattern is fixed, independent of speaker size, then the recognition problem is much simpler than it might otherwise be. If the listener has learned a set of formant-frequency templates for the different vowels of their language, then the perceptual system can determine what the current vowel is simply by shifting each pattern back and forth along the log-wavelength axis in turn to see which of the templates provides the best fit; at the same time, the position of the best fitting template provides a measure of the size of the speaker.

A simple model of vowel perception

The mathematical basis for perception and recognition is provided by rearranging the terms in the production expression

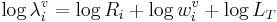(5)

into an expression for the calculation of L_T, namely,

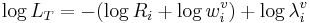. (6)

Conceptually, the R_i and log w_i variables are not part of the perceptual system, and their values are fixed. Thus, in perception, it is likely that they are combined into a simple normalization variable, n_i. In this case the perception calculation becomes

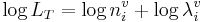, (7)

where .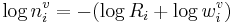

The role of 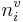in perception is shown in the lower portion of Figure 2. 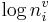converts 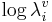, the log of the wavelength of a specific formant of a specific vowel, into log L_T, the log of the sender’s vocal tract length. For a given vowel, there would be three of these wavelength normalizing values, which convert the formant wavelengths into values that converge on L_T. The process is illustrated in the lower panel of Figure 2.

It is this length-convergence property of log n_i that provides the basis for vowel decoding in the covariant, acoustic-scale domain. Imagine that the brain stores its knowledge of vowel sounds as a structure with three rows for each vowel as in Figure 3, and the entries for the formants of the vowel are bars of length 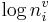. When a vowel occurs, we assume that the log-wavelength values, 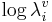, are passed to the memory structure and, for each and every vowel, the individual 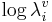values are extended by a length corresponding to the appropriate 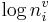value. For most of the vowels, the three normalized lengths will be different, but for one vowel, they will all be the same. This coincidence identifies the vowel type, and the value that the estimates converge on is log L_T. Here then is a bottom up mechanism in which a memory structure can be used to simultaneously decode vowel-type and VTL, using the knowledge that, in the log domain, the representation of the formant-pattern and VTL information is covariant.

Figure 3: A memory structure that can store and decode vowel formant information

A VTL variable for speaker tracking

Finally, imagine the activity that occurs in the memory structure over the course of a sentence as a stream of vowels pass through the decoding mechanism. Assume that when the formant bars line up and identify the vowel type (and VTL), that the ends of the bars light up and together form a small vertical bar (that is, there is some non-linear emphasis of the coincidence). As the sentence progresses, a sequence of vertical bars will light up in a largely random order. However, since the vowels all come from a single speaker, the bars will all occur on the same vertical line, and since the rate of vowels is relatively high relative to short term memory, the alignment of successive bars in the memory structure will providing a clear and continuing estimate of the vocal tract length of the speaker. The estimate is not only independent of vowel type, it is also independent of the pitch and loudness of the voice, which vary over the course of a sentence to provide prosody information. Thus, this formant pattern model not only provides a mechanism for speaker independent recognition of vowel sounds; as a corollary, it provides a method of tracking speakers in multi-source environments using the VTL estimates that flow from the information segregation process.

References

References not in database

Arai, T. (2006). “Sliding three-tube model as a simple educational tool for vowel production,” Acoust. Sci. & Tech. 27, 6